[LUOGU1251]餐巾计划问题

题目

题目描述

一个餐厅在相继的 $N$ 天里,每天需用的餐巾数不尽相同。假设第 $i$ 天需要 $r_i$ 块餐巾( i=1,2,…,N)。餐厅可以购买新的餐巾,每块餐巾的费用为 $p$ 分;或者把旧餐巾送到快洗部,洗一块需 m 天,其费用为 f 分;或者送到慢洗部,洗一块需 $n$ 天$(n>m)$,其费用为 $s$ 分$(s<f)$。

每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。

试设计一个算法为餐厅合理地安排好 $N$ 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。

输入输出格式

输入格式：

由标准输入提供输入数据。文件第 1 行有 1 个正整数 $N$，代表要安排餐巾使用计划的天数。

接下来的 $N$ 行是餐厅在相继的 $N$ 天里,每天需用的餐巾数。

最后一行包含5个正整数$p,m,f,n,s$。$p$ 是每块新餐巾的费用; $m$ 是快洗部洗一块餐巾需用天数; $f$ 是快洗部洗一块餐巾需要的费用; $n$ 是慢洗部洗一块餐巾需用天数; $s$ 是慢洗部洗一块餐巾需要的费用。

输出格式：

将餐厅在相继的 N 天里使用餐巾的最小总花费输出

输入输出样例

输入样例#1：

3
1 7 5 
11 2 2 3 1

输出样例#1：

说明

N<=2000

ri<=10000000

p,f,s<=10000

题解

考虑建立源点和汇点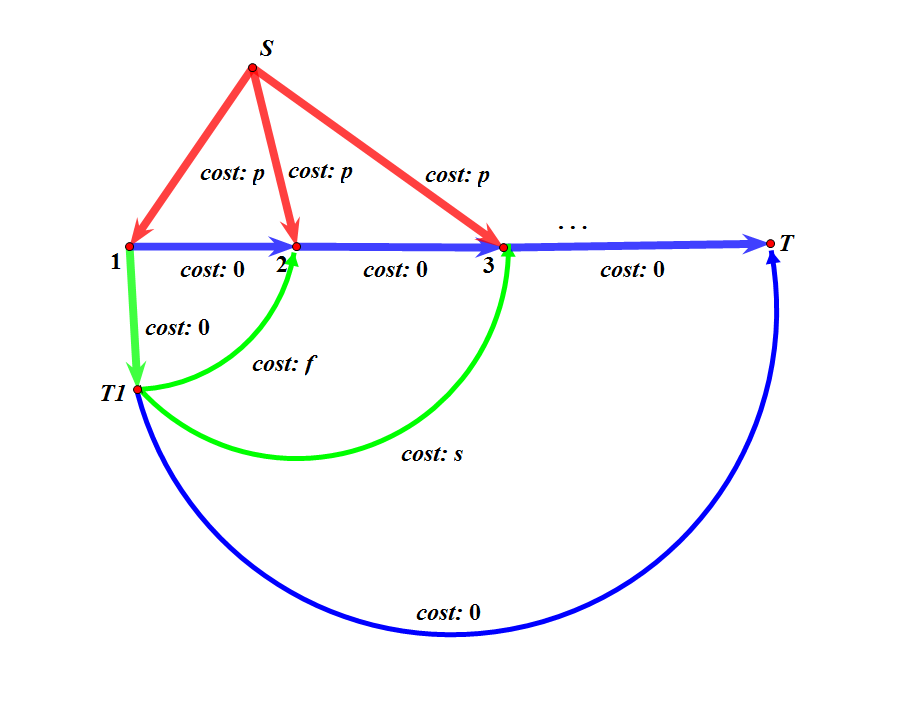如图所示，$S\rightarrow i,i\rightarrow i+1$，拆点出来$i+N$，$i+N$再进行分类，那么边的花费就很显然了

但是流量该设成多少呢？

直接$r_i$是不行的，$r_i$的流量会直接从$i+N$流入汇点$T$

发现问题：餐巾的数量不一定，无法控制$i$天流向$i+m$和$i+n$的流量

可以用$S\rightarrow i+N$表示新买入餐巾，$S\rightarrow i \rightarrow i+N+n \rightarrow T$表示送到快洗部，慢洗同理

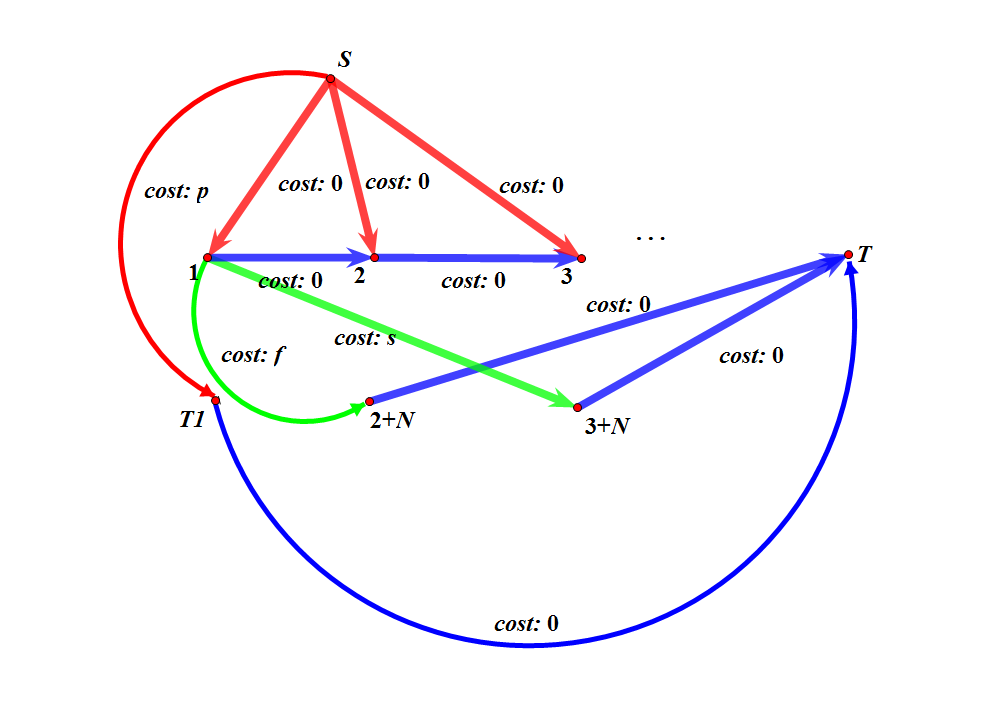
这样边的流量$S\rightarrow i+N,S\rightarrow i$设为$r_i$，其他边因为不确定流量所以统统设成$INF$就好了

代码

# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define LL long long
using namespace std;
const int MAX=5e4+5,t=5e4+1,T=5e4+2,inf=1e8;
struct p{
	int x,y,dis,cn;
}c[MAX];
int n,num=1,id,S,F,P,_n,_m;
int h[MAX],pre[MAX],r[MAX],qu[MAX];
LL d[MAX];
bool use[MAX];
void add(int x,int y,int dis,int cn)
{
	c[++num]=(p){h[x],y,dis,cn},h[x]=num;
	c[++num]=(p){h[y],x,0,-cn},h[y]=num;
}
int read()
{
	int x(0);
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar());
	for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
	return x;
}
LL EK()
{
	int tl,hl;
	LL tot=0;
	while(1)
	{
		memset(d,1,sizeof(d));
		d[0]=0,tl=hl=1;
		while(hl<=tl)
		{
			int tt=qu[hl++];
			use[tt]=0;
			for(int i=h[tt];i;i=c[i].x)
			  if(d[c[i].y]>d[tt]+c[i].cn&&c[i].dis)
			  {
			  	d[c[i].y]=d[tt]+c[i].cn,pre[c[i].y]=i;
			  	if(!use[c[i].y]) qu[++tl]=c[i].y;
			  }
		}
		if(d[T]>1e12) return tot;
		int hh=T,sum=1e9,l;
		while(hh) l=pre[hh],sum=min(c[l].dis,sum),hh=c[l^1].y;
		hh=T;
		while(hh) l=pre[hh],tot+=sum*c[l].cn,c[l].dis-=sum,c[l^1].dis+=sum,hh=c[l^1].y;
	}
}
int main()
{
	n=read();
	for(int i=1;i<=n;++i)
	  {
	  	add(0,i,r[i]=read(),0),add(i+n,T,r[i],0);
	  	if(i!=n) add(i,i+1,inf,0);
	  }
	P=read(),_m=read(),F=read(),_n=read(),S=read();
	for(int i=1;i<=n;++i)
	  {
	  	add(0,i+n,r[i],P);
	  	if(i+_m<=n) add(i,i+_m+n,inf,F);
	  	if(i+_n<=n) add(i,i+_n+n,inf,S);
	  }
	return printf("%lld",EK()),0;
}

题目