题目
题目背景
本题时限2s,内存限制256M
题目描述
在很久很久以前,有一棵n个点的树,每个点有一个点权。
现在有q次操作,每次操作是修改一个点的点权或指定一个点,询问以这个点为根时每棵子树点权和的平方和。
(题目不是很好懂,没看太懂的可以看看样例解释)
输入输出格式
输入格式:
第一行两个整数n、q。
接下来n-1行每行两个整数a和b,表示树中a与b之间有一条边,保证给出的边不会重复。
接下来一行n个整数,第i个整数表示第i个点的点权。
接下来q行每行两或三个数,如果第一个数为1,那么接下来有两个数x和y,表示将第x个点的点权修改为y,如果第一个数为2,那么接下来有一个数x,表示询问以x为根时每棵子树点权和的平方和。
输出格式:
对于每个询问输出答案。
输入输出样例
输入样例#1:
4 5
1 2
2 3
2 4
4 3 2 1
2 2
1 1 3
2 3
1 2 4
2 4
输出样例#1:
121
140
194
说明
样例解释
这是一个菊花图,2与1、3、4间有边。
一开始每个点点权分别为4、3、2、1。
第一个询问以2为根,1、3、4子树中都只有本身一个点,2子树中有所有点,那么1、3、4子树中的点权和就分别是自己的点权4、2、1,2子树中的点权和就是4+3+2+1=10, $4^2+2^2+1^2+10^2=121$。
接下来将第一个点点权修改为3,每个点点权分别为3、3、2、1。
第二个询问以3为根,1、4子树中只有自己,2子树中有1、2、4,3子树中有所有点,1、4子树点权和就是自己的点权3、1,2子树点权和就是3+3+1=7,3子树点权和为3+3+2+1=9,$3^2+1^2+7^2+9^2=140$。
接下来把第二个点点权修改为4,每个点点权分别为3、4、2、1。
第三个询问以4为根,1、3子树点权和就是3和2,2子树点权和就是3+4+2=9,4子树点权和为3+4+2+1=10,$3^2+2^2+9^2+10^2=194$。
数据范围
对于10%的数据,$n,q\leq 2000$。
对于40%的数据,$n,q\leq 60000$。
对于另外30%的数据,保证每次询问的根都为1。
对于100%的数据,$1\leq n,q\leq 200000$,$−10\leq $输入的每个点权$\leq 10$。
建议使用输入优化,虽然标程没加读入优化也能过
题解
神™小清新
看数据,里面有$30\%$的数据保证每次询问根都为$1$
如果一个点点权被修改了,可以看成这个点增加了一个值(比如$5\rightarrow 3$可以看成$5+(-2)=3$)
考虑$a$点点值增加了$x$会对答案有什么影响
增加点值肯定影响的是以$(1,a)$这条路径上的点为根的子树的值,$sum_i$为以$i$为根的子树和
$ans_{now}=ans+\sum_{i\in (1,a)}(sum_i+x)^2-\sum_{i\in (1,a)}sum_i^2$
$=ans+length_{(1,a)}x^2+\sum_{i\in (1,a)}sum_i^2+2x\sum_{i\in (1,a)}sum_i-\sum_{i\in (1,a)}sum_i^2$
$=ans+length_{(1,a)}x^2+2x\sum_{i\in (1,a)}sum_i$
可以看出,需要维护的是$(1,a)$上$sum$的和,需要查询和修改
考虑换根操作,假设换的根为$rt$,$S_i$以$rt$为根时以$i$为根的子树和
可以发现换根只影响$(1,a)$上的点,其他点对答案无影响(画图看看)
对于$(1,a)$上的点$i$,如图:
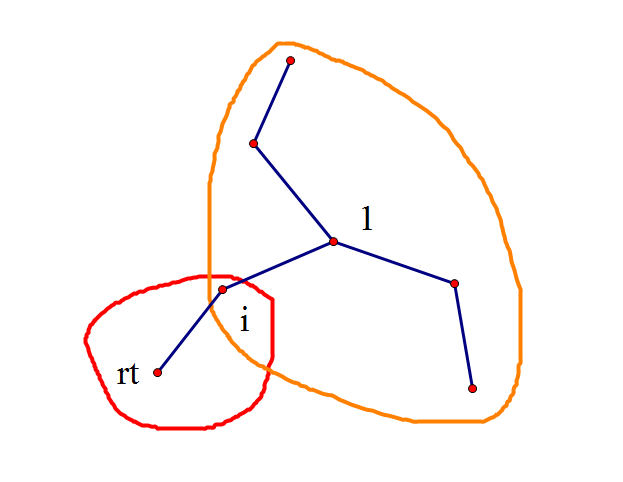
红色部分是$sum_i$,橙色部分是$S_i$,可以发现$sum_i+S_{son_i}=sum_1=S_{rt}$
所以答案变成:
$ans_{rt}=ans+\sum_{i \in (1,rt)}{S_i}^2-\sum_{i \in (1,rt)}{sum_i}^2$
$=ans+{S_{rt}}^2+\sum_{i \in (1,fa_{rt})}{S_i}^2-\sum_{i \in (1,rt)}{sum_i}^2$
$=ans+{sum_1}^2+\sum_{i \in(son_1,rt)}(sum_1-sum_i)^2-\sum_{i\in (1,rt)}{sum_i}^2$
$=ans+(length_{(1,rt)}-1){sum_1}^2-2\times sum_1\sum_{i \in(son(1),rt)}sum_i$
$=ans+sum_1\times ((length_{(1,rt)}-1)sum_1-2\times (\sum_{i \in(1,rt)}sum_i-sum_1))$
$=ans+sum_1\times ((length_{(1,rt)}+1)sum_1-2\times \sum_{i \in(1,rt)}sum_i)$
发现还是需要$(1,a)$上的$sum$的和,还有$sum_1$,修改时维护一下就好了
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define tl (k<<1)
# define tr (k<<1|1)
# define mid (l+r>>1)
# define LL long long
using namespace std;
const int MAX=2e5+1;
struct p{
int x,lazy;
}s[MAX<<2];
struct o{
int x,y;
}c[MAX<<1];
int n,q,num,cnt;
LL ans;
int h[MAX],W1[MAX],w[MAX],son[MAX],siz[MAX],id[MAX],fa[MAX],top[MAX],d[MAX],sum[MAX];
int read()
{
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);f=(ch=='-')?-1:1,ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x*f;
}
void add(int x,int y)
{
c[++num]=(o){h[x],y},h[x]=num;
c[++num]=(o){h[y],x},h[y]=num;
}
void dfs(int x,int f)
{
fa[x]=f,d[x]=d[f]+1,siz[x]=1,sum[x]=w[x];
for(int i=h[x];i;i=c[i].x)
{
int y=c[i].y;
if(y==f) continue;
dfs(y,x);
siz[x]+=siz[y],sum[x]+=sum[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
void dfs1(int x,int tp)
{
ans+=1ll*sum[x]*sum[x],top[x]=tp,W1[id[x]=++cnt]=sum[x];
if(son[x]) dfs1(son[x],tp);
else return;
for(int i=h[x];i;i=c[i].x)
{
int y=c[i].y;
if(y==fa[x]||y==son[x]) continue;
dfs1(y,y);
}
}
void pus(int k)
{
s[k].x=s[tl].x+s[tr].x;
}
void build(int l,int r,int k)
{
if(l==r)
{
s[k].x=W1[l];
return;
}
build(l,mid,tl),build(mid+1,r,tr);
pus(k);
}
void down(int l,int r,int k)
{
if(!s[k].lazy) return;
s[tl].lazy+=s[k].lazy,s[tr].lazy+=s[k].lazy;
s[tl].x+=(mid-l+1)*s[k].lazy,s[tr].x+=(r-mid)*s[k].lazy;
s[k].lazy=0;
}
void change(int l,int r,int k,int L,int R,int dis)
{
if(l==L&&r==R)
{
s[k].x+=(r-l+1)*dis,s[k].lazy+=dis;
return;
}
down(l,r,k);
if(R<=mid) change(l,mid,tl,L,R,dis);
else if(L>mid) change(mid+1,r,tr,L,R,dis);
else change(l,mid,tl,L,mid,dis),change(mid+1,r,tr,mid+1,R,dis);
pus(k);
}
void CHANGE(int x,int dis)
{
while(top[1]!=top[x])
change(1,n,1,id[top[x]],id[x],dis),x=fa[top[x]];
change(1,n,1,1,id[x],dis);
}
LL ask(int l,int r,int k,int L,int R)
{
if(l==L&&r==R) return s[k].x;
down(l,r,k);
if(R<=mid) return ask(l,mid,tl,L,R);
if(L>mid) return ask(mid+1,r,tr,L,R);
return ask(l,mid,tl,L,mid)+ask(mid+1,r,tr,mid+1,R);
}
LL ASK(int x)
{
LL ans=0;
while(top[1]!=top[x])
ans+=ask(1,n,1,id[top[x]],id[x]),x=fa[top[x]];
return ans+ask(1,n,1,1,id[x]);
}
int main()
{
n=read(),q=read();
for(int i=1;i<n;++i)
add(read(),read());
for(int i=1;i<=n;++i)
w[i]=read();
dfs(1,0),dfs1(1,1),build(1,n,1);
int Sum=sum[1];
for(int i=1;i<=q;++i)
{
int op=read(),x=read();
if(op==1)
{
int dis=read(),Dis=dis-w[x];
w[x]=dis,Sum+=Dis;
ans+=1ll*Dis*Dis*(d[x])+2ll*Dis*ASK(x),CHANGE(x,Dis);
}
else if(op==2) printf("%lld\n",ans+1ll*Sum*((d[x]+1)*Sum-2ll*ASK(x)));
}
return 0;
}

