竟然没有$2-SAT$的百度词条 _(:з」∠)
$2-SAT$是一种特殊的逻辑判定问题
emmmm先看一道题:
众所周知,Aufun有很多的Au
不然怎么叫AufunAufun每天最大的乐趣就是把这些Au翻过来翻过去
现在你已经知道m条关于这些Au的信息,每条信息告诉你标号为$X$ Au正/反的时候标号为$Y$ 的Au不能为正/反
Aufun想问问你是否有一种情况ta 的Au满足这些条件,并让你随便构造出一种来
正解:以大量纸片人为交换代价让Aufun代你A这道题
-
构造状态
发现每块Au(点)都有两种状态(正/反)
我们想到每个点可以拆开成两个点,分别代表着一种状态,$x0$表示这个点状态为反,$x1$表示这个点状态为正
emmmm有点了,我们可不可以通过连边来表示点与点之间的关系呢?
如果选了点$A$就必须选点$B$,就从$A$出发连一条单向边到$B$
这样两种状态之间,$A$正面$B$必须反面就可以表示成$A0->B1$
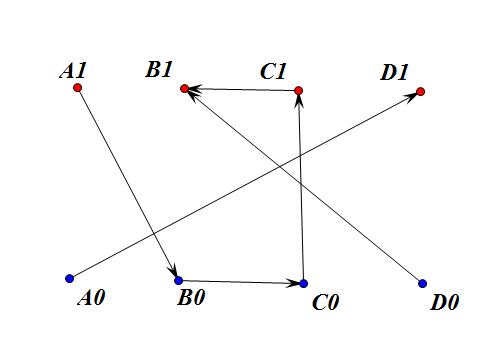
如图,如果按照刚才的方法连边,应该是$A$正面$B$反面,$B$反面$C$反面,$C$反面$C$正面,$C$正面$B$正面,$A$反面$D$正面,$D$反面$B$正面
等等$C$反面$C$正面是什么鬼?
就是$C$反面$C$就必须正面,这样的事情根本不可能你给我搞一个试试,所以$C$必须正面
-
判断方案是否可行
发现点与点之间是单向边,那么我们连着连着就可能出现强连通分量
有什么影响吗?
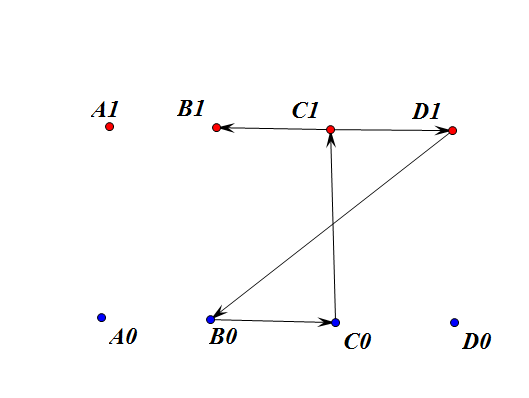
这样构成的一张图,可以看出$B0,C0,C1,D1$在一个强连通分量中,在一个强连通分量说明选了其中一个点其他在同一强连通分量中的点都必须选
这样选$C0$就必须选$C1$,选$C1$也必须选$C0$,这肯定不成立QAQ
所以我们可以通过找强连通分量来判断是否存在可行方案
复杂度:$O(m)$($m$为连边数量)
-
输出方案
因为$A$连$B$表示选$A$必须选$B$,所以$A$的拓扑序肯定大于$B$
注意这里是选$A$就必须选$B$,但是选$B$不一定选$A$
所以对于每个点的两种状态,可以选拓扑序大的,舍弃掉另一个(选一个就不能选另一个了)
每个点都判断与对立点谁的拓扑序大
注意这里可以不用再搞一遍拓扑排序,因为$Tarjan$求强连通分量每个点所在的强连通分量编号可以代替拓扑序
编号和拓扑序是相反的,即要每两对点找编号小的
输出每个点状态就行了
-
其他情况
两个点的关系还有很多,列举几个(这里存在和不存在是一个点的两种状态):
$A,B$不能同时存在:$A\rightarrow B’,B\rightarrow A’$
$A,B$必须同时存在:$A\rightarrow B,A’\rightarrow B’$
$A,B$必须存在其中一个:$A’\rightarrow B,B’\rightarrow A$
$A,B$不能同时存在:$A\rightarrow B’,B\rightarrow A’$
$A$不能存在:$A\rightarrow A’$
-
输出方案 二连击
上面的输出方案是随意输出一种即可,但是要是要求输出字典序最小的答案呢?
也是很好解决的,$dfs$即可
点从$1\sim 2n$枚举,如果这个点能选,就将ta相连的点都选上,就将ta相连的点的相连的点都选上,就将…
如果某个点发生冲突了(对立点被选了),这个点就不能选,与ta相连的点不能选,与ta相连的点的相连点不能选,与ta…
这样最后被选中的点就是这字典序最小的解了,复杂度:$O(nm)$
发现我大部分在水字数啊emmmm
几道例题
似乎字数还不够我再水水选一道题讲讲qwq
上面的第三题,是按$A$和$B$不能同时存在建边的
但是通过拓扑序很难判断三种状态
考虑$dfs$当前点的某个状态对应的点,表示必须选这个状态,如果对立状态也被选中,说明这个点不能选,否则说明这个点可以被选
这样$dfs$一个点的两个状态所对应的点
如果两个状态都能被选,说明这个点可选可不选;如果两个状态都不能选,说明没法构造出可行的方案,输出$IMPOSSIBLE$;如果某个状态可选,对立状态不可被选,说明这个点必须选这个状态
部分代码
void dfs(int x)//use表示是否选这个点
{
use[x]=1;
for(int i=h[x];i;i=c[i].x)
if(!use[c[i].y]) dfs(c[i].y);
}
bool look(int x)
{
memset(use,0,sizeof(use));
dfs(x);//选择这个点和ta后面的点
for(int i=1;i<=n;++i)
if(use[i]&&use[i+n]) return 0;//判断方法还是一样的,如果两个状态都被选了说明不可行
return 1;
}
int main()
{
scanf("%d%d",&n,&m);
//构造图过程略去
for(int i=1;i<=n;++i)
{
bool d1=look(i),d2=look(i+n);//判断两个状态
if(!d1&&!d2) return printf("IMPOSSIBLE"),0;
if(d1&&d2) ans[i]='?';
if(d1&&!d2) ans[i]='N';
if(!d1&&d2) ans[i]='Y';//记录每种情况
}
for(int i=1;i<=n;++i)
printf("%c",ans[i]);
return 0;
}
再看一下第二道题水到200行
很显然$a,b,c$场地分别对应两种车,符合$2-SAT$的要求
这个是按$A,B$必须同时存在建边的,比如说$(i,h_i,j,h_j)$为$(1,c,5,a)$,则将1场地的$c$状态$->$5场地的$a$状态
但是$x$场地对应三种车怎么办呢?
发现$x$场地的个数很少,最大才$8$个
所以考虑枚举$x$场地的状态,比如这次可以让$x$场地对应$AB$车(就成了$c$场地),下次对应$BC$车(就成了$a$场地),再下次对应$AC$车(就成了$b$场地)
这样复杂度是$O(3^{8}\times (n+m))$,仍然过不了这道题
发现$x$对应AC车的情况在前面两个枚举中都出现了,也就是说前面两个枚举把所有情况都包括了
所以只用枚举前两个就行了,复杂度$O(2^{8}\times (n+m))$
部分代码
bool look()//枚举x状态进行判断是否可行
{
memset(h,0,sizeof(h));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
num=0,Col=0;
for(int i=1;i<=m;++i)
{
if(S[s[i].i]==s[i].hi+32) continue;//S是场地字符串,s是给定4元组
int tt=s[i].hi+32==pos[0][s[i].i]?s[i].i:s[i].i+n;//pos为每个点代表的两个状态
if(S[s[i].j]==s[i].hj+32) add(tt,re[tt]);//re为对立点
else
{
int ttt=s[i].hj+32==pos[0][s[i].j]?s[i].j:s[i].j+n;
add(tt,ttt),add(re[ttt],re[tt]);
}
}
for(int i=1;i<=2*n;++i)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i)
if(col[i]==col[i+n]) return 0;
return print(),1;
}
注意:中间那里是判断$j$处是否能被选(这里能被选的意思是没有条件限制的$j$处场地适合开这个车)
如果能被选,就按$A,B$必须同时存在连边;否则说明不能选这个四元组,就按$A$不能存在连边
这下字数应该水够了qwq

