题目
题目描述
小 S 现在拥有 $n$ 座城市，第 $i$ 座城市的人口为 $w_i$，城市与城市之间可能有双向道路相连。
现在小 S 要将这 $n$ 座城市划分成若干个州，每个州由至少一个城市组成，每个城市在恰好一个州内。
假设小 S 将这些城市划分成了 $k$ 个州，设 $V_i$ 是第 $i$ 个州包含的所有城市组成的集合。定义一条道路是一个州的内部道路，当且仅当这条道路的两个端点城市都在这个州内。如果一个州内部存在一条起点终点相同，不经过任何不属于这个州的城市，且经过这个州的所有内部道路都恰好一次并且经过这个州的所有城市至少一次的路径（路径长度可以为 $0$），则称这个州是不合法的。
定义第 $i$ 个州的满意度为：第 $i$ 个州的人口在前 $i$ 个州的人口中所占比例的 $p$ 次幂，即：
$\left (\frac{\sum_{x \in V_i}{w_x}}{\sum_{j=1}^{i}\sum_{x \in V_j}{w_x}}\right )^p$
定义一个划分的满意度为所有州的满意度的乘积。
求所有合法的划分方案的满意度之和。
答案对 $998244353$ 取模。 两个划分 ${V_1…V_k}$ 和 ${C_1…C_s}$ 是不同的，当且仅当 $k \neq s$，或存在某个 $1 \leq i \leq k$，使得 $V_i \neq C_i$。
输入输出格式
输入格式：
从文件 ${\tt walk.in}$ 中读入数据。
输入第一行包含三个整数 $n,m,p$，表示城市个数、城市之间的道路个数以及题目描述中的常数 $p$。
接下来 $m$ 行，每行两个正整数 $u,v$，描述一条无向的道路，保证无重边无自环。
输入第 $m+2$ 行有 $n$ 个正整数，第 $i$ 个正整数表示 $w_i$。
输出格式：
输出到文件 ${\tt walk.out}$ 中。
输出一行一个整数表示答案在模 $998244353$ 意义下的取值。
即设答案化为最简分式后的形式为 $a/b$ ，其中 $a$ 和 $b$ 的互质。输出整数 $x$ 使得 $bx \equiv a\mod 998244353$ 且 $0 \leq x < 998244353$。可以证明这样的整数 $x$ 是唯一的。
输入输出样例
输入样例#1：
3 2 1
1 2
2 3
1 1 1
输出样例#1：
1
说明
【提示】
$x^{p-1} \equiv 1\mod p$，其中 $p$ 为质数， $x \in [1,p)$。
【子任务】
（注：表中测试点为子任务）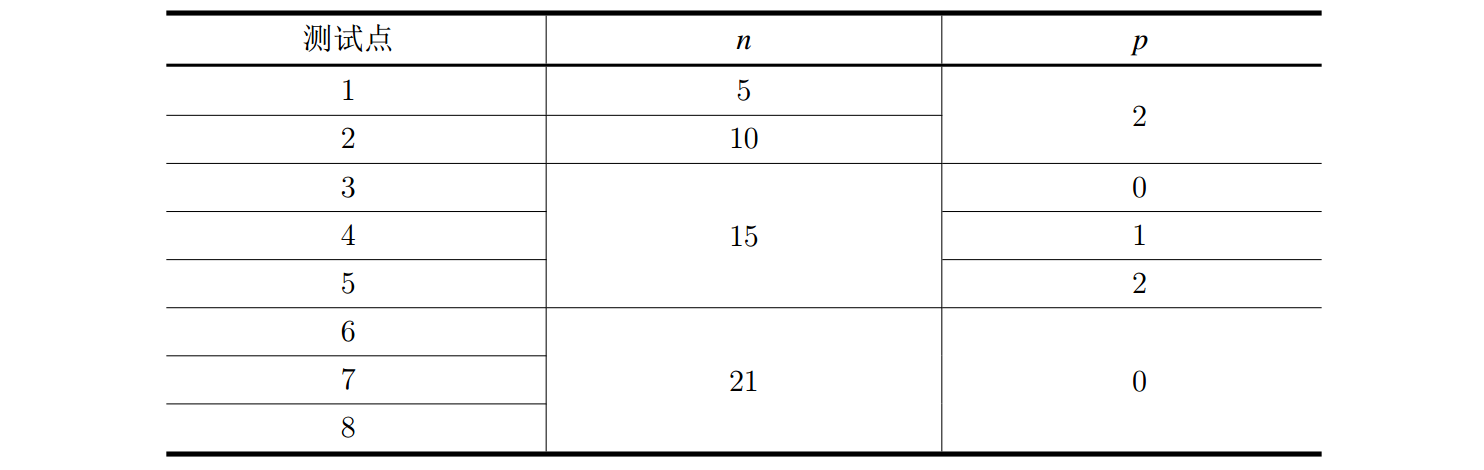 
本题共$20$个测试点，每个子任务对应测试点如下（与表中不符之处已注明）：
子任务$1$对应测试点$1$；
子任务$2$对应测试点$2$；
子任务$3$对应测试点$3$；
子任务$4$对应测试点$4$；
子任务$5$对应测试点$5$；
子任务$6$对应测试点$6-10$（$n=21,p=0$）；
子任务$7$对应测试点$11-16$（$n=21,p=1$）；
子任务$8$对应测试点$17-20$（$n=21,p=2$）；
保证对于所有数据有： $0 \leq n \leq 21$，$0 \leq m \leq n*(n-1)/2$ ， $0 \leq p \leq 2$， $1 \leq w_i \leq 100$。
题解
题目中州不合法的限制就是一个州中的点全部连通并且存在欧拉回路
状压表示每一种情况，$f_S$表示城市集合为$S$时的答案，有$dp$方程：$f_S=\frac{1}{\sum_{i\in S}w_i}\sum_{T\subset S}f_{S-T}\times \sum_{i\in T}w_i$，其中保证$T$合法
后面的东西一脸可以卷积的样子……但是$or$卷积不能保证$S-T$和$T$中没有重复的部分
设$f_{i,S}$表示城市集合为$S$且有$i$个城市的答案，然后对于每一个$i$，$f_i(x)=\sum_{k+j=i}f_k(x)g_j(x)$
常数好大……
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
using namespace std;
const int MAX=(1<<21),mod=998244353;
int n,m,P,lim;
int fa[21],du[21],W[MAX],w[21],a[21],lW[MAX];
int f[22][MAX],g[22][MAX];
int Pow(int a,int b)
{
int ans=1;
for(;b;b>>=1,a=1ll*a*a%mod)
if(b&1) ans=1ll*ans*a%mod;
return ans;
}
int find(int x)
{
if(fa[x]!=x) fa[x]=find(fa[x]);
return fa[x];
}
int GET_NUM(int x)
{
int num=0;
while(x) x&=x-1,++num;
return num;
}
void FWT(int *A,int tt=1)
{
for(int i=1;i<lim;i<<=1)
for(int l=i<<1,j=0;j<lim;j+=l)
for(int k=0;k<i;++k)
if(tt==1) A[i+j+k]=(A[j+k]+A[i+j+k])%mod;
else A[i+j+k]=(A[i+j+k]-A[j+k]+mod)%mod;
}
int main()
{
scanf("%d%d%d",&n,&m,&P),lim=1<<n;
for(int i=1,x,y;i<=m;++i)
scanf("%d%d",&x,&y),a[x-1]|=(1<<y-1),a[y-1]|=(1<<x-1);
for(int i=0;i<n;++i)
scanf("%d",&w[i]);
for(int s=1,x;s<lim;++s)
{
x=GET_NUM(s);
for(int i=0;i<n;++i)
{
fa[i]=i,du[i]=0;
if(s&(1<<i)) W[s]+=w[i];
}
for(int i=0;i<n;++i)
if(s&(1<<i)) for(int j=i+1;j<n;++j)
if((a[i]&(1<<j))&&(s&(1<<j)))
{
++du[i],++du[j];
if(find(i)!=find(j)) fa[find(i)]=find(j);
}
if(P==2) W[s]=1ll*W[s]*W[s]%mod;
else if(!P) W[s]=1;
lW[s]=Pow(W[s],mod-2);
int RT=-1;
for(int i=0;i<n;++i)
if(s&(1<<i)) if(RT==-1) RT=find(i);
else if(RT!=find(i)) {RT=-2;break;}
if(RT==-2) g[x][s]=W[s];
else
{
bool fl=0;
for(int i=0;i<n;++i)
if(s&(1<<i)) if(du[i]%2) {fl=1;break;}
if(fl) g[x][s]=W[s];
}
}
f[0][0]=1;
for(int i=1;i<=n;++i)
{
FWT(g[i]),FWT(f[i-1]);
for(int j=0;j<i;++j)
for(int k=0;k<lim;++k)
(f[i][k]+=1ll*f[j][k]*g[i-j][k]%mod)%=mod;
FWT(f[i],-1);
for(int j=0;j<lim;++j)
if(f[i][j]) f[i][j]=1ll*f[i][j]*lW[j]%mod;
}
return printf("%d",f[n][lim-1]),0;
}
