[湖南集训]谈笑风生 - A-Failure的博客

题目

题目描述

设 T 为一棵有根树，我们做如下的定义：

• 设 a 和 b 为 T 中的两个不同节点。如果 a 是 b 的祖先，那么称“a 比 b 不知道高明到哪里去了”。

• 设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x，那么称“a 与 b 谈笑风生”。

给定一棵 n 个节点的有根树 T，节点的编号为 1 ∼ n，根节点为 1 号节点。你需要回答 q 个询问，询问给定两个整数 p 和 k，问有多少个有序三元组 (a; b; c) 满足：

a、 b 和 c 为 T 中三个不同的点，且 a 为 p 号节点；
a 和 b 都比 c 不知道高明到哪里去了；
a 和 b 谈笑风生。这里谈笑风生中的常数为给定的 k。

输入输出格式

输入格式：

输入文件的第一行含有两个正整数 n 和 q，分别代表有根树的点数与询问的个数。

接下来 n − 1 行，每行描述一条树上的边。每行含有两个整数 u 和 v，代表在节点 u 和 v 之间有一条边。

接下来 q 行，每行描述一个操作。第 i 行含有两个整数，分别表示第 i 个询问的 p 和 k。

输出格式：

输出 q 行，每行对应一个询问，代表询问的答案。

输入输出样例

输入样例#1：

输出样例#1：

3
1
3

说明

样例中的树如下图所示：

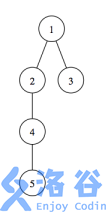
对于第一个和第三个询问，合法的三元组有 (2,1,4)、 (2,1,5) 和 (2,4,5)。

对于第二个询问，合法的三元组只有 (4,2,5)。

所有测试点的数据规模如下：

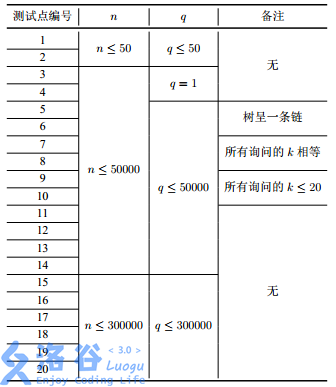
对于全部测试数据的所有询问， 1 ≤ p ≤ n， 1 ≤ k ≤ n.

题解

只有两种情况满足条件：

$b$为$a$的祖先，$c$在$a$的子树里
$a$为$b$的祖先，$c$在$b$的子树里

第一种情况可以直接算，第二种情况对$dfs$序建主席树即可

代码

# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define tl s[k].l
# define tr s[k].r
# define mid (l+r>>1)
# define LL long long
using namespace std;
const int MAX=3e5+5;
struct p{
	int l,r;
	LL x;
}s[MAX<<5];
struct q{
	int x,y;
}c[MAX<<1];
int n,Q,tot,cnt,num;
int siz[MAX],h[MAX],id[MAX],d[MAX],rt[MAX],re[MAX];
int read()
{
	int x(0);
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar());
	for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
	return x;
}
void add(int x,int y)
{
	c[++num]=(q){h[x],y},h[x]=num;
	c[++num]=(q){h[y],x},h[y]=num;
}
void change(int l,int r,int &k,int pre,int x,int d)
{
	s[k=++tot]=s[pre],s[k].x+=d;
	if(l==r) return;
	if(x<=mid) change(l,mid,tl,s[pre].l,x,d);
	else change(mid+1,r,tr,s[pre].r,x,d);
}
LL ask(int l,int r,int k,int pre,int L,int R)
{
	if(r<L||R<l) return 0;
	if(l>=L&&r<=R) return s[pre].x-s[k].x;
	return ask(l,mid,tl,s[pre].l,L,R)+ask(mid+1,r,tr,s[pre].r,L,R);
}
void dfs(int x=1,int fa=0)
{
	siz[x]=1,re[id[x]=++cnt]=x,d[x]=d[fa]+1;
	for(int i=h[x];i;i=c[i].x)
	  if(c[i].y^fa) dfs(c[i].y,x),siz[x]+=siz[c[i].y];
}
int main()
{
	n=read(),Q=read();
	for(int i=1;i<n;++i)
	  add(read(),read());
	dfs();
	for(int i=1;i<=n;++i)
	  change(1,n,rt[i],rt[i-1],d[re[i]],siz[re[i]]-1);
	for(int i=1,x,k;i<=Q;++i)
	  x=read(),k=read(),printf("%lld\n",1ll*min(d[x]-1,k)*(siz[x]-1)+ask(1,n,rt[id[x]],rt[id[x]+siz[x]-1],d[x]+1,d[x]+k));
	return 0;
}

题目