题目
题目描述
Anihc 国有 $n$ 个城市,这 $n$ 个城市从 $1\sim n$ 编号,$1$ 号城市为首都。城市间初始时有 $m$ 条高速公路,每条高速公路都有一个非负整数的经济影响因子,每条高速公路的两端都是城市(可能两端是同一个城市),保证任意两个城市都可以通过高速公路互达。
Anihc 国正在筹划「八纵八横」的高铁建设计划,计划要修建一些高速铁路,每条高速铁路两端也都是城市(可能两端是同一个城市),也都有一个非负整数的经济影响因子。国家还计划在「八纵八横」计划建成之后,将「一带一路」扩展为「一带一路一环」,增加「内陆城市经济环」即选择一条从首都出发沿若一系列高铁与高速公路走的路径,每条高铁或高速公路可以经过多次,每座城市也可以经过多次,最后路径又在首都结束。令「内陆城市经济环」的 GDP 为依次将这条路径上所经过的高铁或高速公路的经济影响因子异或起来(一条路经过多次则会被计算多次)。
现在 Anihc 在会议上讨论「八纵八横」的建设计划方案,他们会不断地修改计划方案,希望你能实时反馈对于当前的「八纵八横」的建设计划的方案「内陆城市经济环」的最大是多少。
初始时,八纵八横计划中不包含任何—条高铁,有以下三种操作:
Add x y z
在计划中给在城市 $x$ 和城市 $y$ 之间建设一条高铁,其经济影响因子为 $z$ ,如果这是第 $k$ 个 Add 操作,则将这条高铁命名为 $k$ 号高铁。
Cancel k
将计划中的 $k$ 号高铁取消掉,保证此时 号高铁一定存在。
Change k z
表示将第 $k$ 号高铁的经济影响因子更改为 $z$ ,保证此时 $k$ 号高铁一定存在。
输入格式
第一行三个整数 $n$ , $m$ , $P$ ,表示城市个数,高速公路条数,操作个数。
接下来 $m$ 行,每行三个整数表示高速公路的信息。
接下来 $P$ 行,每行为一个操作。
注意:输入的所有经济影响因子都将以二进制的形式从高位到低位给出。
输出格式
第一行一个整数,表示如果不修建任何高铁,「内陆城市经济环」的 GDP 最大值。
接下 $P$ 行,每行一个整数表示进行了对应的每一个操作之后,对于当前的计划「内陆城市经济环」的 GDP 最大值。
注意:输出的答案也要以二进制的形式从高位到低位给出。
样例
样例输入
4 4 3
1 2 1110
1 3 10
2 4 1110
2 3 100
Add 3 4 11
Change 1 101
Cancel 1
样例输出
1000
1001
1111
1000
数据范围与提示
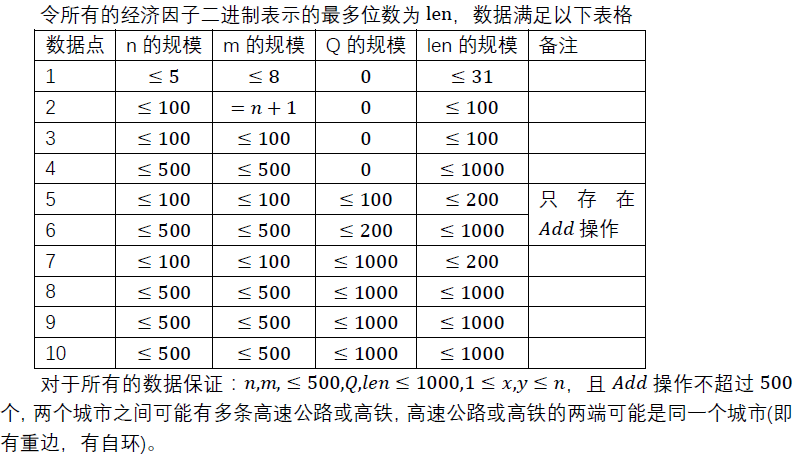
注,Add 操作次数不超过$550$次。
题解
首先不管加入新边,先求初始的答案
是不是跟这题很像?
只用找出图中的环放进线性基求最大值即可
后面加入、删除、修改新边的操作可以看成每条边有一个存在时间区间
一说到存在时间区间,我就想到线段树分治
对于一条新加的边,把它形成的环加入线段树对应节点,然后一路加到叶子再求解即可
开始没想到可以用bitset优化操作emmmm
注意运算效率
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<vector>
# include<bitset>
# include<algorithm>
# define X first
# define Y second
# define tl (k<<1)
# define tr (k<<1|1)
# define mid (l+r>>1)
# define mp make_pair
# define BT bitset<MAX>
# define Pi pair<int,BT>
using namespace std;
const int MAX=1e3+5;
struct q{
int x,y,ti;
BT d;
}a[MAX];
int n,m,P,N,cnt;
bool use[MAX];
char b[MAX];
BT em,ans;
BT d[MAX];
vector<Pi> vec[MAX];
vector<BT> s[MAX<<2];
BT max(BT A,BT B)
{
for(int i=N;i>=0;--i)
if(A[i]^B[i]) return A[i]?A:B;
return A;
}
struct Base{
BT p[MAX];
void ins(BT A)
{
for(int i=N;i>=0;--i)
if(A[i])
{
if(!p[i].any()) return void(p[i]=A);
A=A^p[i];
}
}
BT ask()
{
BT ans=em;
for(int i=N;i>=0;--i)
if(p[i].any()&&!ans[i]) ans^=p[i];
return ans;
}
}qwq;
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
void dfs(int x=1,int fa=0)
{
use[x]=1;
for(int i=0,cnt=vec[x].size(),y;i<cnt;++i)
if(vec[x][i].X^fa)
{
y=vec[x][i].X;
if(use[y]) qwq.ins(d[x]^d[y]^vec[x][i].Y);
else d[y]=d[x]^vec[x][i].Y,dfs(y,x);
}
}
BT GET_BIT(char *a)
{
BT A=em;
int len;
N=max(N,len=strlen(a)-1);
for(int i=len;i>=0;--i)
A[len-i]=a[i]-'0';
return A;
}
BT Read() {return scanf("%s",b),GET_BIT(b);}
void add(int x,int y,BT d) {vec[x].push_back(mp(y,d)),vec[y].push_back(mp(x,d));}
void change(int l,int r,int k,int L,int R,BT d)
{
if(r<L||R<l) return;
if(l>=L&&r<=R) return void(s[k].push_back(d));
change(l,mid,tl,L,R,d),change(mid+1,r,tr,L,R,d);
}
void Solve(int l=1,int r=P,int k=1,Base x=qwq)
{
if(l>r) return;
for(int i=0,cnt=s[k].size();i<cnt;++i)
x.ins(s[k][i]);
if(l==r)
{
ans=x.ask();
bool fl=0;
for(int i=N;i>=0;--i)
{
if(ans[i]) fl=1;
if(fl) ans[i]?printf("%d",1):printf("0");
}
printf("\n");
}
else Solve(l,mid,tl,x),Solve(mid+1,r,tr,x);
}
int main()
{
n=read(),m=read(),P=read();
for(int i=1,x,y;i<=m;++i)
x=read(),y=read(),add(x,y,Read());
dfs(),ans=qwq.ask();
bool fl=0;
for(int i=N;i>=0;--i)
{
if(ans[i]) fl=1;
if(fl) ans[i]?printf("%d",1):printf("0");
}
printf("\n");
for(int i=1,x,y;i<=P;++i)
{
scanf("%s",b);
BT D;
if(b[0]=='A') x=read(),y=read(),D=Read(),a[++cnt]=(q){x,y,i,D};
else if(b[1]=='a') x=read(),change(1,P,1,a[x].ti,i-1,d[a[x].x]^a[x].d^d[a[x].y]),a[x].ti=-1;
else if(b[1]=='h') x=read(),D=Read(),change(1,P,1,a[x].ti,i-1,d[a[x].x]^a[x].d^d[a[x].y]),a[x].d=D,a[x].ti=i;
}
for(int i=1;i<=cnt;++i)
if(a[i].ti!=-1) change(1,P,1,a[i].ti,P,d[a[i].x]^a[i].d^d[a[i].y]);
return Solve(),0;
}

