[SHOI2012]信用卡凸包 - A-Failure的博客

题目

题目背景

SHOI2012D1T2

题目描述

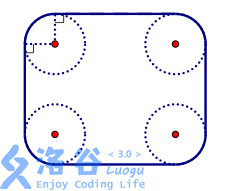
信用卡是一个矩形，唯四个角作了圆滑处理，使它们都是与矩形的两边相切的 1/4 圆，如下图所示。现在平面上有一些规格相同的信用卡，试求其凸包的周长。注意凸包未必是多边形，因为它可能包含若干段圆弧。

输入输出格式

输入格式：

输入的第一行是一个正整数 n，表示信用卡的张数。第二行包含三个实数 a, b, r，分别表示信用卡（圆滑处理前）竖直方向的长度、水平方向的长度，以及 1/4 圆的半径。

之后 n 行，每行包含三个实数 x, y, θ，分别表示一张信用卡中心（即对角线交点）的横、纵坐标，以及绕中心逆时针旋转的弧度。

输出格式：

输出只有一行，包含一个实数，表示凸包的周长，四舍五入精确到小数点后2 位。

输入输样例

输入样例#1：

2
6.0 2.0 0.0
0.0 0.0 0.0
2.0 -2.0 1.5707963268

输出样例#1：

21.66

输入样例#2：

3
6.0 6.0 1.0
4.0 4.0 0.0
0.0 8.0 0.0
0.0 0.0 0.0

输出样例#2：

41.60

输入样例#3：

3
6.0 6.0 1.0
4.0 4.0 0.1745329252
0.0 8.0 0.3490658504
0.0 0.0 0.5235987756

输出样例#3：

41.63

说明

样例1说明：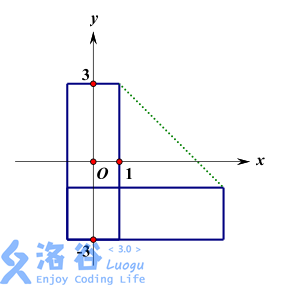

本样例中的 2 张信用卡的轮廓在上图中用实线标出，如果视 1.5707963268为pi/2，那么凸包的周长为16+4sqrt(2)

样例2说明：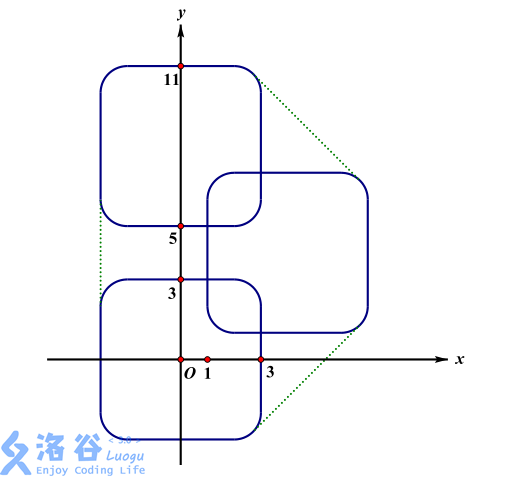

样例3说明：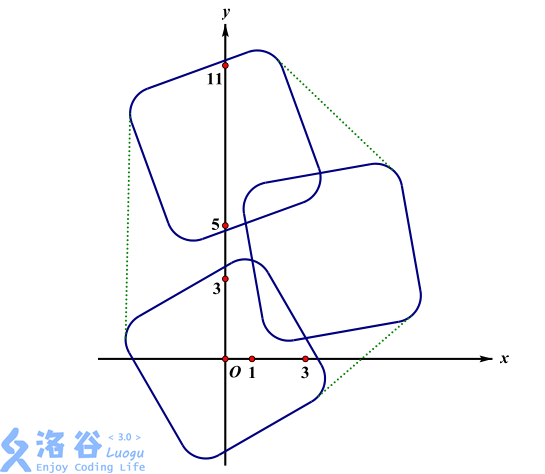

其凸包的周长约为41.628267652。

本题可能需要使用数学库中的三角函数。不熟悉使用方法的选手，可以参考下面的程序及其输出结果：

uses math;
const Pi = 3.141592653589793;
begin
writeln(sin(30.0 / 180.0 * Pi) : 0 : 10);
writeln(cos(60.0 / 180.0 * Pi) : 0 : 10);
writeln(tan(45.0 / 180.0 * Pi) : 0 : 10);
writeln(arcsin(1.0) : 0 : 10);
writeln(arccos(0.0) : 0 : 10);
writeln(arctan(1.0) : 0 : 10);
end.
#include <iostream>
#include <math.h>
using namespace std;
const double Pi = 3.141592653589793;
int main()
{
cout.setf(ios::fixed);
cout.precision(10);
cout<<sin(30.0 / 180.0 * Pi)<<endl;
cout<<cos(60.0 / 180.0 * Pi)<<endl;
cout<<tan(45.0 / 180.0 * Pi)<<endl;
cout<<asin(1.0)<<endl;
cout<<acos(0.0)<<endl;
cout<<atan(1.0)<<endl;
return 0;
}

输出结果：0.5000000000

0.5000000000

1.0000000000

1.5707963268

0.7853981634

数据范围：

题解

把圆弧去掉，线段往里面合，最后能合成一个凸包

同时圆弧合起来能合成一个圆

所以就是所有信用卡的四角求一个凸包周长，最后加上一个圆的周长即可

代码

# include<iostream>
# include<cstring>
# include<cstdio>
# include<cmath>
# include<algorithm>
using namespace std;
const int MAX=1e5+5;
const double fs=1e-6;
struct Point{
	double x,y;
	Point(double X=0,double Y=0) {x=X,y=Y;}
	bool operator< (const Point &a)
	const{
		if(x!=a.x) return x<a.x;
		return y<a.y;
	}
}_P[MAX];
Point operator+ (Point a,Point b) {return Point(a.x+b.x,a.y+b.y);}
Point operator- (Point a,Point b) {return Point(a.x-b.x,a.y-b.y);}
Point operator* (Point a,double b) {return Point(a.x*b,a.y*b);}
int n,cnt,Top;
double r,a,b,ans;
double Cross(Point x,Point y) {return x.x*y.y-y.x*x.y;}
double Cmp(Point a,Point b,Point c) {return Cross(b-a,c-a);}
bool cmp(Point a,Point b)
{
	if(fabs(Cmp(_P[1],a,b))<fs) return a.x<b.x;
	return Cmp(_P[1],a,b)>0;
}
double GET_DIS(Point a,Point b) {return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
int st[MAX];
int main()
{
	scanf("%d%lf%lf%lf",&n,&a,&b,&r);
	for(int i=1;i<=n;++i)
	  {
	  	double x,y,R;
	  	scanf("%lf%lf%lf",&x,&y,&R);
	  	_P[++cnt]=(Point(cos(R),sin(R))*(b/2-r))+(Point(-sin(R),cos(R))*(a/2-r))+Point(x,y);
	  	_P[++cnt]=(Point(cos(R),sin(R))*(-(b/2-r)))+(Point(-sin(R),cos(R))*(a/2-r))+Point(x,y);
	  	_P[++cnt]=(Point(cos(R),sin(R))*(-(b/2-r)))+(Point(-sin(R),cos(R))*(-(a/2-r)))+Point(x,y);
	  	_P[++cnt]=(Point(cos(R),sin(R))*(b/2-r))+(Point(-sin(R),cos(R))*(-(a/2-r)))+Point(x,y);
	  }
	sort(_P+1,_P+1+cnt),st[Top=1]=1,sort(_P+2,_P+1+cnt,cmp);
	for(int i=2;i<=cnt;++i)
	  {
	  	while(Top>1&&Cross(_P[st[Top]]-_P[st[Top-1]],_P[i]-_P[st[Top]])<=0) --Top;
		st[++Top]=i;
	  } 
	for(int i=2;i<=Top;++i)
	  ans+=GET_DIS(_P[st[i]],_P[st[i-1]]);
	return printf("%.2lf",ans+GET_DIS(_P[st[Top]],_P[1])+2*r*acos(-1.0)),0;
}

题目