题目
题目描述
魔咒串由许多魔咒字符组成,魔咒字符可以用数字表示。例如可以将魔咒字符 1、2 拼凑起来形成一个魔咒串 [1,2]。
一个魔咒串 S 的非空字串被称为魔咒串 S 的生成魔咒。
例如 S=[1,2,1] 时,它的生成魔咒有 [1]、[2]、[1,2]、[2,1]、[1,2,1] 五种。S=[1,1,1] 时,它的生成魔咒有 [1]、[1,1]、[1,1,1] 三种。最初 S 为空串。共进行 n 次操作,每次操作是在 S 的结尾加入一个魔咒字符。每次操作后都需要求出,当前的魔咒串 S 共有多少种生成魔咒。
输入输出格式
输入格式:
第一行一个整数 n。
第二行 n 个数,第 i 个数表示第 i 次操作加入的魔咒字符。
输出格式:
输出 n 行,每行一个数。第 i 行的数表示第 i 次操作后 S 的生成魔咒数量
输入输出样例
输入样例#1:
7
1 2 3 3 3 1 2
输出样例#1:
1
3
6
9
12
17
22
说明
对于%10的数据,$1 \le n \le 10$
对于%30的数据,$1 \le n \le 100$
对于%60的数据,$1 \le n \le 1000$
对于%100的数据,$1 \le n \le 100000$
用来表示魔咒字符的数字 $x$ 满足$1 \le x \le 10^9$
题解
如果字符串固定,答案就是$\frac{n(n+1)}{2}-\sum_{i=1}^{n}height_i$,考虑维护后面的$height$和
如果加入一个字符,就相当于生成了一个新的后缀,ta对于答案的贡献就是与上一个排名的$height$取$min$,同时减去上一个排名原来右方向的贡献,下一个排名同理
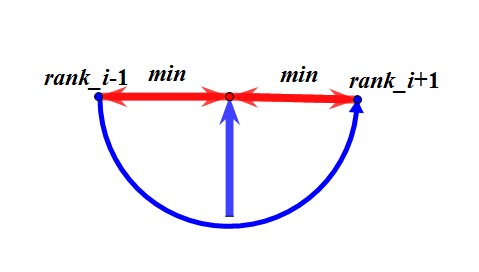
如图,红箭头(取$min$)表示加上的值,蓝箭头表示减去的值
用set维护一下就好了
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<set>
# include<algorithm>
# define LL long long
using namespace std;
const int MAX=1e5+5;
struct p{
int x,id;
bool operator< (const p &a)
const{
return x<a.x;
}
}A[MAX];
int n,m,cnt,id;
LL ans;
int a[MAX],tax[MAX],h[MAX],het[MAX],rk[MAX],sa[MAX],Log[MAX],L[MAX],R[MAX];
int f[21][MAX];
set<int> s,s1;
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
bool cmp(int *a,int x,int y,int w) {return a[x]==a[y]&&a[x+w]==a[y+w];}
void rsort()
{
for(int i=0;i<=m;++i)
tax[i]=0;
for(int i=1;i<=n;++i)
++tax[rk[h[i]]];
for(int i=1;i<=m;++i)
tax[i]+=tax[i-1];
for(int i=n;i>=1;--i)
sa[tax[rk[h[i]]]--]=h[i];
}
void Suffix()
{
for(int i=1;i<=n;++i)
rk[i]=a[i-1],h[i]=i;
m=id+1,rsort();
for(int p=1,w=1,i;p<n;w+=w,m=p)
{
for(p=0,i=n-w+1;i<=n;++i)
h[++p]=i;
for(i=1;i<=n;++i)
if(sa[i]>w) h[++p]=sa[i]-w;
rsort(),swap(rk,h),rk[sa[1]]=p=1;
for(i=2;i<=n;++i)
rk[sa[i]]=cmp(h,sa[i],sa[i-1],w)?p:++p;
}
int j,k=0;
for(int i=1;i<=n;het[rk[i++]]=k)
for(k=k?k-1:k,j=sa[rk[i]-1];a[j+k-1]==a[i+k-1];++k);
}
int GET_LCP(int l,int r)
{
int t=Log[r-l];
return min(f[t][l+1],f[t][r-(1<<t)+1]);
}
void Init()
{
for(int i=1;i<=n;++i)
f[0][i]=het[i];
for(int i=1;i<=20;++i)
for(int j=1;j<=n;++j)
f[i][j]=min(f[i-1][j],f[i-1][min(n,j+(1<<(i-1)))]);
}
int main()
{
n=read(),Log[0]=-1;
for(int i=1;i<=n;++i)
a[i-1]=read(),Log[i]=Log[i>>1]+1;
reverse(a,a+n);
for(int i=1;i<=n;++i)
A[i]=(p){a[i-1],i-1};
sort(A+1,A+1+n);
for(int i=1;i<=n;++i)
{
if(A[i].x!=A[i-1].x) ++id;
a[A[i].id]=id;
}
Suffix(),Init();
for(int i=n,x;i>=1;--i)
{
set<int>::iterator T1=s.lower_bound(rk[i]),T2=s1.lower_bound(-rk[i]);
if(T1!=s.end()) ans+=(x=GET_LCP(rk[i],*T1))-L[*T1],L[*T1]=x;
if(T2!=s1.end()) ans+=(x=GET_LCP(-*T2,rk[i]))-R[-*T2],R[-*T2]=x;
s.insert(rk[i]),s1.insert(-rk[i]),printf("%lld\n",1ll*((n-i+1)*(n-i+2)>>1)-ans);
}
return 0;
}
$fuge$的$O(nlog^2n)$做法……
考虑新加入一个字符的贡献
加入$i$时,如果没有重复子串,对答案的贡献应该是$i$
如果存在$x$,使得$[x,i]$这一段子串在$[1,i-1]$中出现过,那么$[k,i] (x\le k< i)$肯定也在$[1,i-1]$中出现过
所以这个东西符合单调性,可以二分$x$,然后找到$rank$上的最小值不小于$i-x+1$的区间,用主席树判断是否可行即可
嗯,显然这东西即难写还跑得慢,最高得分是$Asia$疯狂卡常$90$分
代码
## include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define tl s[k].l
# define tr s[k].r
# define mid (l+r>>1)
# define LL long long
using namespace std;
const int MAX=1e5+5;
struct p{
int x,l,r;
}s[MAX<<5];
struct q{
int x,id;
bool operator< (const q &a)
const{
return x<a.x;
}
}A[MAX];
int n,m,id,tot;
LL ans;
int h[MAX],het[MAX],tax[MAX],Log[MAX],rk[MAX],sa[MAX],a[MAX],rt[MAX];
int f[21][MAX];
bool fl;
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
bool cmp(int *a,int x,int y,int w) {return a[x]==a[y]&&a[x+w]==a[y+w];}
void rsort()
{
for(int i=0;i<=m;++i)
tax[i]=0;
for(int i=1;i<=n;++i)
++tax[rk[h[i]]];
for(int i=1;i<=m;++i)
tax[i]+=tax[i-1];
for(int i=n;i>=1;--i)
sa[tax[rk[h[i]]]--]=h[i];
}
void Suffix()
{
for(int i=1;i<=n;++i)
rk[i]=a[i],h[i]=i;
m=id+1,rsort();
for(int p=1,w=1,i;p<n;w+=w,m=p)
{
for(p=0,i=n-w+1;i<=n;++i)
h[++p]=i;
for(i=1;i<=n;++i)
if(sa[i]>w) h[++p]=sa[i]-w;
rsort(),swap(rk,h),rk[sa[1]]=p=1;
for(i=2;i<=n;++i)
rk[sa[i]]=cmp(h,sa[i],sa[i-1],w)?p:++p;
}
int j,k=0;
for(int i=1;i<=n;het[rk[i++]]=k)
for(k=k?k-1:k,j=sa[rk[i]-1];a[j+k]==a[i+k];++k);
}
int change(int pre,int l,int r,int x)
{
int k=++tot;
s[k]=s[pre],++s[k].x;
if(l==r) return k;
if(x<=mid) tl=change(s[pre].l,l,mid,x);
else tr=change(s[pre].r,mid+1,r,x);
return k;
}
int ask(int l,int r,int k,int L,int R)
{
if(fl) return 1;
if(l>R||L>r) return 0;
if(l>=L&&r<=R) return fl=s[k].x;
return ask(l,mid,tl,L,R)+ask(mid+1,r,tr,L,R);
}
int GET_LCP(int l,int r)
{
if(l==r) return n-sa[l]+1;
int t=Log[r-l];
return min(f[t][l+1],f[t][r-(1<<t)+1]);
}
void Init()
{
Log[0]=-1;
for(int i=1;i<=n;++i)
Log[i]=Log[i>>1]+1,f[0][i]=het[i],rt[i]=change(rt[i-1],1,n,rk[i]);
for(int i=1;i<=20;++i)
for(int j=1;j<=n;++j)
f[i][j]=min(f[i-1][j],f[i-1][min(n,j+(1<<(i-1)))]);
}
bool look(int L,int x)
{
fl=0;
int __L=x-L+1,_L,_R,ans=rk[L],l=rk[L],r=n;
while(l<=r)
{
if(GET_LCP(rk[L],mid)>=__L) ans=mid,l=mid+1;
else r=mid-1;
}
_R=ans,l=1,r=ans=rk[L];
while(l<=r)
{
if(GET_LCP(mid,rk[L])>=__L) ans=mid,r=mid-1;
else l=mid+1;
}
_L=ans;
return ask(1,n,rt[x-__L],_L,_R);
}
int main()
{
n=read();
for(int i=1;i<=n;++i)
A[i]=(q){a[i]=read(),i};
sort(A+1,A+1+n);
for(int i=1;i<=n;++i)
{
if(A[i].x!=A[i-1].x) ++id;
a[A[i].id]=id;
}
Suffix(),Init();
for(int i=1,l,r,Ans;i<=n;++i)
{
l=1,r=i,Ans=i;
while(l<=r)
{
if(look(mid,i)) Ans=mid,r=mid-1;
else l=mid+1;
}
ans+=Ans-look(Ans,i),printf("%lld\n",ans);
}
return 0;
}

