题目
题目描述
为了提高智商,ZJY准备去往一个新世界去旅游。这个世界的城市布局像一棵树。每两座城市之间只有一条路径可以互达。每座城市都有一种宝石,有一定的价格。ZJY为了赚取最高利益,她会选择从A城市买入再转手卖到B城市。由于ZJY买宝石时经常卖萌,因而凡是ZJY路过的城市,这座城市的宝石价格会上涨。让我们来算算ZJY旅游完之后能够赚取的最大利润。(如a城市宝石价格为v,则ZJY出售价格也为v)
输入输出格式
输入格式:
第一行输入一个正整数N表示城市个数
接下来一行输入N个正整数表示每座城市宝石的最初价格p,每个宝石的初始价格不超过100。
第三行开始连续输入N-1行,每行有两个数字x和y。表示x城市和y城市有一条路径。城市编号从1开始。下一行输入一个正整数Q表示询问次数。
接下来Q行每行输入三个正整数a,b,v,表示ZY从a旅游到b,城市宝石上涨v。
输出格式:
对于每次询问,输出ZJY可能获得的最大利润,如果亏本了则输出0。
输入输出样例
输入样例#1:
3
1 2 3
1 2
2 3
2
1 2 100
1 3 100
输出样例#1:
1
1
说明
数据范围
对于30%的数据,有0 < N ≤ 100, 0 < Q ≤ 10000。
对于100%的数据,有0 < N ≤ 50000, 0 < Q ≤ 50000。
题解
出题人这个语文表达能力真的……
题目大意:
给定一棵树,每次询问从$a$走到$b$,选择两个城市$c,d(dis_{a,c}<dis_{a,d})$,使得$w_d-w_c$的值最大,求这个最大值,并且要求维护链上修改
如果是一个序列,显然用线段树就可以简单维护,这是放到树上的,所以用树链剖分维护了
考虑树链剖分处理询问的过程,两点深度大的往上沿着重链跳,直到跳到$LCA$
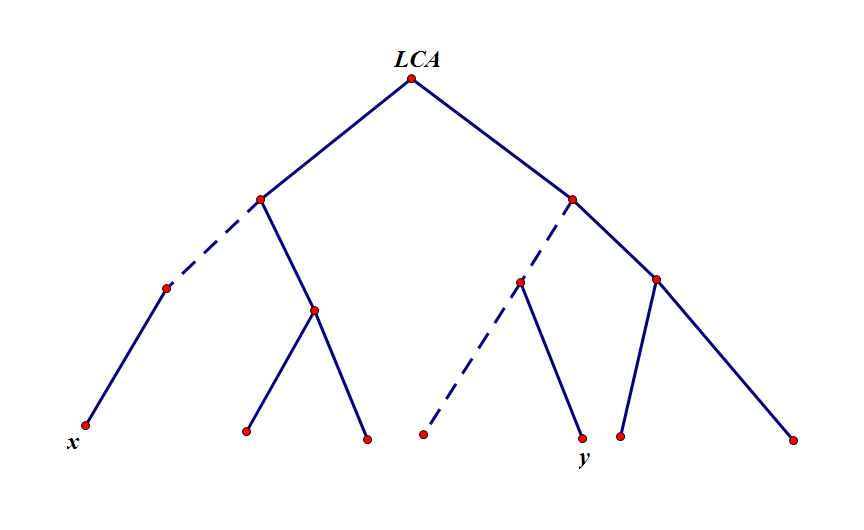
这样有两个问题:
- 一条链上不一定是一个编号连续的区间
- 左边链是由大的编号(线段树编号)跳到小的编号
所以要分左右链讨论,对于第一个问题,在跳链的时候维护一个最大(右边链)最小(左边链)值即可;对于第二个问题,在线段树上同时维护从左到右和从右到左的最大差值即可
对树链剖分跳链分情况讨论好像还挺常见的qwq
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define tl (k<<1)
# define tr (k<<1|1)
# define mid (l+r>>1)
using namespace std;
const int MAX=5e4+5;
struct p{
int minn,maxn,d,_d,tag;
p(){d=_d=-2e9;}
}s[MAX<<2];
struct q{
int x,y;
}c[MAX<<1];
int n,m,num,cnt;
int h[MAX],d[MAX],f[MAX],siz[MAX],son[MAX],w[MAX],re[MAX],top[MAX],id[MAX];
int read()
{
int x=0,fl=1;
char ch=getchar();
for(;!isdigit(ch);fl=(ch=='-')?-1:1,ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x*fl;
}
void add()
{
int x=read(),y=read();
c[++num]=(q){h[x],y},h[x]=num;
c[++num]=(q){h[y],x},h[y]=num;
}
void dfs(int x=1,int fa=0)
{
f[x]=fa,d[x]=d[fa]+(siz[x]=1);
for(int i=h[x];i;i=c[i].x)
if(c[i].y^fa)
{
dfs(c[i].y,x),siz[x]+=siz[c[i].y];
if(siz[son[x]]<siz[c[i].y]) son[x]=c[i].y;
}
}
void dfs1(int x=1,int tp=1)
{
top[x]=tp,id[x]=++cnt,re[cnt]=x;
if(!son[x]) return;
dfs1(son[x],tp);
for(int i=h[x];i;i=c[i].x)
if((c[i].y^f[x])&&(c[i].y^son[x])) dfs1(c[i].y,c[i].y);
}
p pus(p b,p c,int Tag=0)
{
p a;
a.minn=min(b.minn,c.minn);
a.maxn=max(b.maxn,c.maxn);
a.d=max(c.maxn-b.minn,max(b.d,c.d));
a._d=max(b.maxn-c.minn,max(b._d,c._d));
return a.tag=Tag,a;
}
void build(int l=1,int r=n,int k=1)
{
if(l==r) return void(s[k].minn=s[k].maxn=w[re[l]]);
build(l,mid,tl),build(mid+1,r,tr),s[k]=pus(s[tl],s[tr]);
}
void down(int k)
{
if(!s[k].tag) return;
int f=s[k].tag;
s[k].tag=0,s[tl].tag+=f,s[tr].tag+=f,s[tl].minn+=f,s[tl].maxn+=f,s[tr].minn+=f,s[tr].maxn+=f;
}
void change(int l,int r,int k,int L,int R,int dis)
{
if(l==L&&r==R)
{
s[k].minn+=dis,s[k].maxn+=dis;
return void(s[k].tag+=dis);
}
down(k);
if(R<=mid) change(l,mid,tl,L,R,dis);
else if(L>mid) change(mid+1,r,tr,L,R,dis);
else change(l,mid,tl,L,mid,dis),change(mid+1,r,tr,mid+1,R,dis);
s[k]=pus(s[tl],s[tr],s[k].tag);
}
void CHANGE(int x,int y,int dis)
{
while(top[x]^top[y])
{
if(d[top[x]]<d[top[y]]) swap(x,y);
change(1,n,1,id[top[x]],id[x],dis),x=f[top[x]];
}
if(d[x]>d[y]) swap(x,y);
change(1,n,1,id[x],id[y],dis);
}
p ask(int l,int r,int k,int L,int R)
{
if(l==L&&r==R) return s[k];
down(k);
if(R<=mid) return ask(l,mid,tl,L,R);
if(L>mid) return ask(mid+1,r,tr,L,R);
return pus(ask(l,mid,tl,L,mid),ask(mid+1,r,tr,mid+1,R));
}
int ASK(int x,int y)
{
int ans=0,maxn_l=-2e9,maxn_r=-2e9,minn_r=2e9,minn_l=2e9;
p tt;
while(top[x]^top[y])
{
if(d[top[x]]<d[top[y]])
{
tt=ask(1,n,1,id[top[y]],id[y]),y=f[top[y]];
ans=max(ans,max(tt.d,maxn_r-tt.minn)),maxn_r=max(maxn_r,tt.maxn),minn_r=min(minn_r,tt.minn);
}
else
{
tt=ask(1,n,1,id[top[x]],id[x]),x=f[top[x]];
ans=max(ans,max(tt._d,tt.maxn-minn_l)),maxn_l=max(maxn_l,tt.maxn),minn_l=min(minn_l,tt.minn);
}
}
if(d[x]>d[y])
{
tt=ask(1,n,1,id[y],id[x]);
ans=max(ans,max(tt._d,tt.maxn-minn_l)),minn_l=min(minn_l,tt.minn);
}
else
{
tt=ask(1,n,1,id[x],id[y]);
ans=max(ans,max(tt.d,maxn_r-tt.minn)),maxn_r=max(maxn_r,tt.maxn);
}
return max(ans,maxn_r-minn_l);
}
int main()
{
n=read();
for(int i=1;i<=n;++i)
w[i]=read();
for(int i=1;i<n;++i,add());
dfs(),dfs1(),build(),m=read();
for(int i=1,a,b,c;i<=m;++i)
a=read(),b=read(),c=read(),printf("%d\n",ASK(a,b)),CHANGE(a,b,c);
return 0;
}

