题目
题目描述
老C是个程序员。
作为一个懒惰的程序员,老C经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的R行C列网格上,如果两个小方格有公共的边,就称它们是相邻的,而且有些相邻的小方格之间的公共边比较特殊。特殊的公共边排列得有很强的规律。首先规定,第1行的前两个小方格之间的边是特殊边。然后,特殊边在水平方向上每4个小方格为一个周期,在竖直方向上每2个小方格为一个周期。所有的奇数列与下一列之间都有特殊边,且所在行的编号从左到右奇偶交替。
下图所示是一个R=C=8的网格,蓝色标注的边是特殊边。首先,在第1行,第1列和第2列之间有一条特殊边。因为竖直方向周期为2,所以所有的奇数行,第1列和第2列之间都有特殊边。因为水平方向周期为4,所以所有奇数行的第5列和第6列之间也有特殊边,如果网格足够大,所有奇数行的第9列和第10列、第13列和第14列之间都有特殊边。因为所有的奇数列和下一列之间都有特殊边,所以第3列和第4列、第7列和第8列之间也有特殊边,而所在行的编号从左到右奇偶交替,所以它们的特殊边在偶数行。如果网格的规模更大,我们可以用同样的方法找出所有的特殊边。
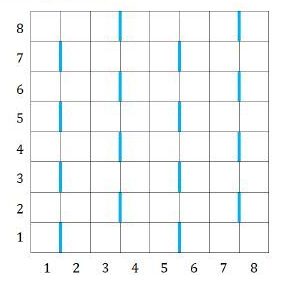
网格的每个小方格刚好可以放入一个小方块,在游戏的一开始,有些小方格已经放上了小方块,另外的小方格没有放。老C很讨厌下图所示的图形,如果他发现有一些小方块排列成了它讨厌的形状(特殊边的位置也要如图中所示),就很容易弃疗,即使是经过任意次旋转、翻转后排列成讨厌的形状,老C也同样容易弃疗。
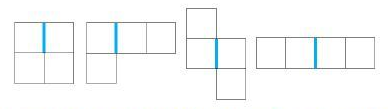
为了防止弃疗,老C决定趁自己还没有弃疗,赶紧移除一些格子里小方块,使得剩下的小方块不能构成它讨厌的形状。但是游戏里每移除一个方块都是要花费一些金币的,每个方块需要花费的金币有多有少参差不齐。老C当然希望尽可能少的使用游戏里的金币,但是最少要花费多少金币呢?老C懒得思考,就把这个问题交给你了。
输入输出格式
输入格式:
第一行有3个正整数C,R,n,表示C列R行的网格中,有n个小方格放了小方块。接下来n行,每行3个正整数x,y,w,表示在第x列第y行的小方格里放了小方块,移除它需要花费w个金币。保证不会重复,且都在网格范围内。
输出格式:
输出一行,包含一个整数,表示最少花费的金币数量。
输入输出样例
输入样例#1:
2 2 4
1 1 5
1 2 6
2 1 7
2 2 8
输出样例#1:
5
输入样例#2:
3 3 7
1 1 10
1 2 15
1 3 10
2 1 10
2 2 10
2 3 10
3 1 10
输出样例#2:
15
说明
【输入输出样例 1 说明】
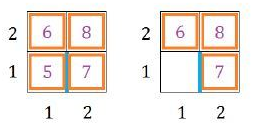
【输入输出样例 2 说明】
如图所示。容易发现,如果不移除第1列第2行的小方块,则至少要移除两个小方块,才能不包含老 C 讨厌的图形,花费至少20个金币;而删除第1列第2行 的小方块后,原有的讨厌图形全都不存在了,只需要 花费15个金币。
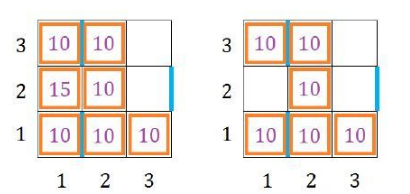
【数据规模与约定】
对于第 1~2 个测试点,1 ≤ C, R ≤ 100, 1 ≤ n ≤ 20;
对于第 3~6 个测试点,1 ≤ C, R ≤ 10^5, 2000 ≤ n ≤ 5000,数据有梯度;
对于第 7~10 个测试点,1 ≤ C, R ≤ 10^5, 30000 ≤ n ≤ 10^5,数据有梯度;
对于所有测试点,1 ≤ C, R, n ≤ 10^5, 1 ≤ w ≤ 10^4。
题解
观察讨厌图形,因为经过任意次旋转、翻转后排列是讨厌图形的也是讨厌图形,所以有这么种情况:
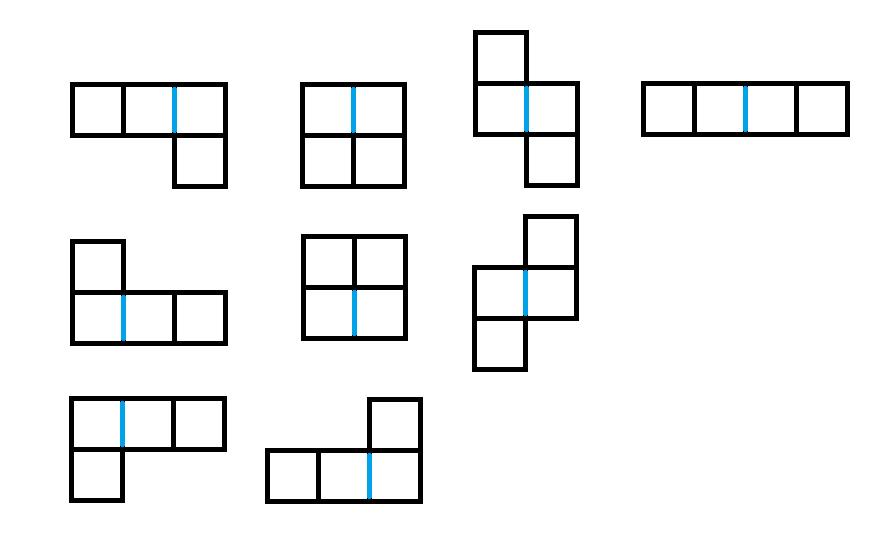
发现是与中心线两边的方块(下面称为中心块)相连的方块分别选个的所有情况,如果把棋盘黑白染色的话:
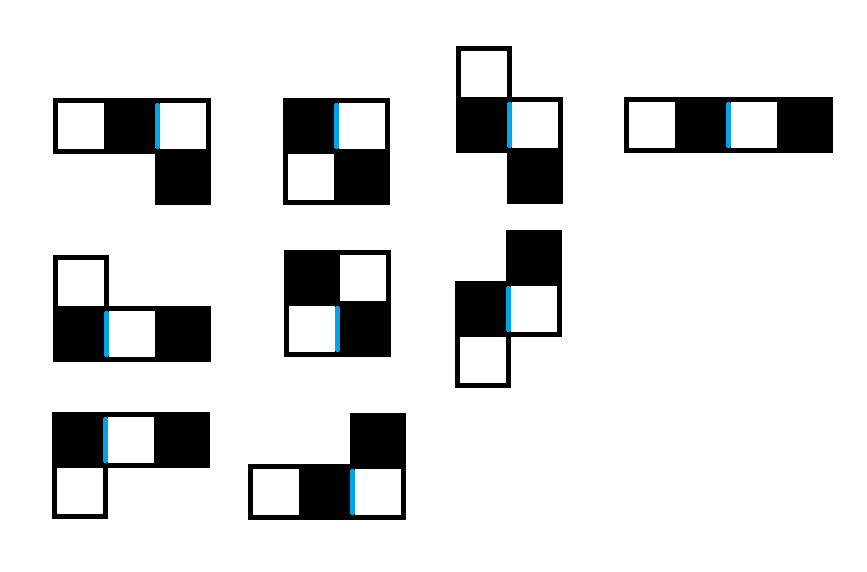
发现与中心块相连的方块颜色与中心块相反
所以考虑最小割,每个中心块一定不会成为别的中心块相连的方块,对于破坏一个讨厌图形,有种选择:
- 去掉两个中心块中的任意一个(两个都去掉肯定不是最优的)
- 去掉与左边中心块相连的所有方块
- 去掉与右边中心块相连的所有方块
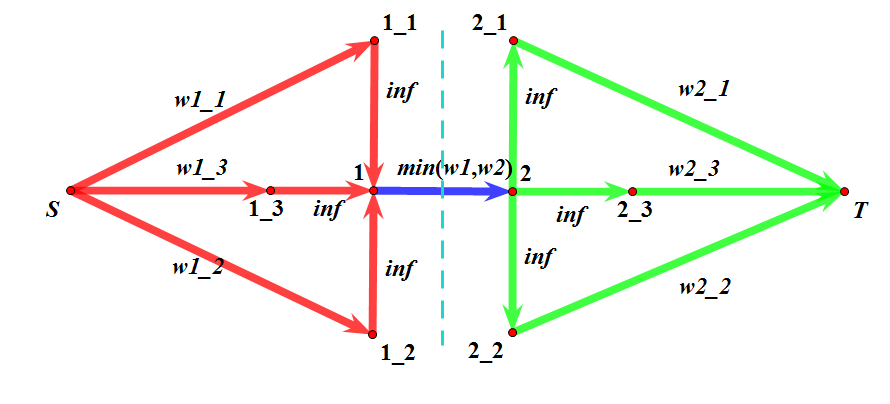
之后就是进行选决策了,建立最小割模型即可
用map存的坐标,虽然比较慢但是比较好写qaq
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<map>
# include<algorithm>
using namespace std;
const int MAX=5e5+5,inf=1e9;
struct p{
int x,y,dis;
}c[MAX];
struct q{
int x,y,w;
}a[MAX];
int n,m,num=1,T,N;
int h[MAX],H[MAX],d[MAX],qu[MAX];
bool use[MAX];
map<pair<int,int>,int> ma;
void add(int x,int y,int dis)
{
if(x==0)
{
if(!use[y]) use[y]=1;
else return;
}
if(y==T)
{
if(!use[x]) use[x]=1;
else return;
}
c[++num]=(p){h[x],y,dis},h[x]=num;
c[++num]=(p){h[y],x,0},h[y]=num;
}
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
bool bfs()
{
memset(d,0,sizeof(d));
int hl=1,tl=d[0]=1;
while(hl<=tl)
{
int tt=qu[hl++];
for(int i=h[tt];i;i=c[i].x)
if(!d[c[i].y]&&c[i].dis) d[c[i].y]=d[tt]+1,qu[++tl]=c[i].y;
}
return d[T];
}
int dfs(int x=0,int dix=inf)
{
if(x==T||!dix) return dix;
int sum=0;
for(int &i=H[x];i;i=c[i].x)
if(d[c[i].y]==d[x]+1&&c[i].dis)
{
int dis=dfs(c[i].y,min(dix,c[i].dis));
if(dis)
{
c[i].dis-=dis,c[i^1].dis+=dis,sum+=dis,dix-=dis;
if(!dix) break;
}
}
if(!sum) d[x]=-2;
return sum;
}
int Dinic()
{
int tot=0,D;
while(bfs())
{
memcpy(H,h,sizeof(H));
while(D=dfs()) tot+=D;
}
return tot;
}
int main()
{
n=read(),m=read(),N=read(),T=N+1;
for(int i=1;i<=N;++i)
a[i].y=read(),a[i].x=read(),a[i].w=read(),ma[make_pair(a[i].x,a[i].y)]=i;
for(int i=1;i<=N;++i)
{
if(a[i].x&1)
{
if(a[i].y%4==1)
{
int qwq=ma[make_pair(a[i].x,a[i].y+1)];
if(qwq)
{
pair<int,int> P1=make_pair(a[i].x,a[i].y-1),P2=make_pair(a[i].x-1,a[i].y),P3=make_pair(a[i].x+1,a[i].y);
int qaq=ma[P1],qvq=ma[P2],qcq=ma[P3];
if(qaq||qvq||qcq)
{
pair<int,int> P4=make_pair(a[i].x,a[i].y+2),P5=make_pair(a[i].x-1,a[i].y+1),P6=make_pair(a[i].x+1,a[i].y+1);
int qnq=ma[P4],quq=ma[P5],qoq=ma[P6];
if(!qnq&&!quq&&!qoq) continue;
add(i,qwq,min(a[i].w,a[qwq].w));
if(qaq) add(0,qaq,a[qaq].w),add(qaq,i,inf);
if(qvq) add(0,qvq,a[qvq].w),add(qvq,i,inf);
if(qcq) add(0,qcq,a[qcq].w),add(qcq,i,inf);
if(qnq) add(qnq,T,a[qnq].w),add(qwq,qnq,inf);
if(quq) add(quq,T,a[quq].w),add(qwq,quq,inf);
if(qoq) add(qoq,T,a[qoq].w),add(qwq,qoq,inf);
}
}
}
}
else
{
if(a[i].y%4==3)
{
int qwq=ma[make_pair(a[i].x,a[i].y+1)];
if(qwq)
{
pair<int,int> P1=make_pair(a[i].x,a[i].y-1),P2=make_pair(a[i].x-1,a[i].y),P3=make_pair(a[i].x+1,a[i].y);
int qaq=ma[P1],qvq=ma[P2],qcq=ma[P3];
if(qaq||qvq||qcq)
{
pair<int,int> P4=make_pair(a[i].x,a[i].y+2),P5=make_pair(a[i].x-1,a[i].y+1),P6=make_pair(a[i].x+1,a[i].y+1);
int qnq=ma[P4],quq=ma[P5],qoq=ma[P6];
if(!qnq&&!quq&&!qoq) continue;
add(qwq,i,min(a[i].w,a[qwq].w));
if(qaq) add(qaq,T,a[qaq].w),add(i,qaq,inf);
if(qvq) add(qvq,T,a[qvq].w),add(i,qvq,inf);
if(qcq) add(qcq,T,a[qcq].w),add(i,qcq,inf);
if(qnq) add(0,qnq,a[qnq].w),add(qnq,qwq,inf);
if(quq) add(0,quq,a[quq].w),add(quq,qwq,inf);
if(qoq) add(0,qoq,a[qoq].w),add(qoq,qwq,inf);
}
}
}
}
}
return printf("%d",Dinic()),0;
}

