[ZROI367]陈太阳与路径

题目

题目描述

陈太阳说要有树，这个世界便有了树。陈太阳说要有一棵$n$个节点的树，一棵随机选择的$n$个节点的有标号树便被召唤了出来。陈太阳说，要对于每个节点，计算出它是多少条路径的中点，答案便浮现在了每个节点旁。但是你没有陈太阳那么强，你只能写个程序计算这些答案了。

一条$x$到$y$的路径，若其包含奇数条边，那么就没有中点。否则设这条路径有$m$条边，那么它的中点就是从$x$向$y$走$\frac{m}{2}$条边后达到的点。$x$到$y$的路径与$y$到$x$的路径视为同一条路径。路径长度可以为$0$。

输入格式

第一行一个整数$n$，表示这棵树的节点个数。

接下来$n-1$行，每行两个整数$x，y$，表示有一条连接$x$和$y$的边。保证这棵树是从所有$n$个节点的有标号树中等概率随机生成的。

输出格式

输出一行$n$个整数，第$i$个数表示表示标号为$i$的点作为多少条路径的中点。

样例1

input

output

2 1 5 1 2 1

数据规模与约定

对于5%的数据保证$n \le 1$

对于10%的数据保证$n \le 100$

对于20%的数据保证$n \le 1000$

对于30%的数据保证$n \le 5000$

对于50%的数据保证$n \le 50000$

对于60%的数据保证$n \le 100000$

对于80%的数据保证$n \le 200000$

对于90%的数据保证$n \le 300000$

对于100%的数据保证$1 \le n \le 500000$

时间限制：$1s$

空间限制：$1GB$

提示

本题的随机树使用随机的prufer序列生成。

题解

对于一棵树，一条路径有三种情况：

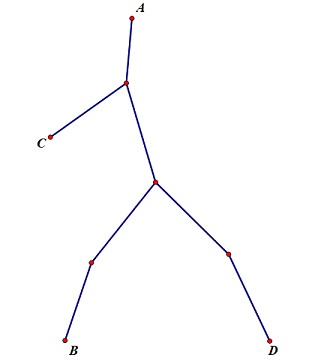
$A\rightarrow B$
$B\rightarrow D$（在同一子树）
$B\rightarrow C,C\rightarrow D$（不在同一子树）

用$f_{i,j}$表示以$i$为根的子树中从$i$出发，长度为$j$的路径条数，可以一遍$dfs$解决第二种情况

用$g_{i,j}$表示从$i$出发，先走一步到父亲，然后随便走的长度为$j$的路径条数，发现ta和$f_{i,j}$有关系，向上走一步再走到父亲的子树里找路径即$f_{fa_i,j-1}$，但是这样包含了向上走一步然后回到$i$的情况，相当于要减去$f_{i,j-2}$（当然$j<2$就不用考虑了）

另一种情况是向上走一步接着向上走（到父亲的父亲），可以用$g_{fa_i,j-1}$表示

所以$g_{i,j}=g_{fa_i,j-1}+f_{fa_i,j-1}-f_{i,j-2}$

因为是用$prufer$序列生成的，树最大深度为$\sqrt n$，普通数组是开不下的，所以用vector维护一下即可

$dls$：这题用长链剖分也能做啊

告辞

代码

# include<iostream>
# include<cstring>
# include<cstdio>
# include<vector> 
# include<algorithm>
# define LL long long
using namespace std;
const int MAX=5e5+5;
struct p{
	int x,y;
}c[MAX<<1];
int n,num;
int h[MAX],fa[MAX],d[MAX];
LL ans[MAX];
vector<int> f[2][MAX];
int read()
{
	int x(0);
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar());
	for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
	return x;
}
void add()
{
	int x=read(),y=read();
	c[++num]=(p){h[x],y},h[x]=num;
	c[++num]=(p){h[y],x},h[y]=num;
}
void dfs(int x=1,int F=0)
{
	fa[x]=F;
	for(int i=h[x];i;i=c[i].x)
	  if(c[i].y!=F) dfs(c[i].y,x),d[x]=max(d[x],d[c[i].y]);
	++d[x],f[0][x].resize(d[x]),f[1][x].resize(d[x]),f[0][x][0]=f[1][x][0]=1;
	for(int i=h[x];i;i=c[i].x)
	  if(c[i].y!=F) for(int j=1;j<=d[c[i].y];++j)
	    ans[x]+=1ll*f[0][x][j]*f[0][c[i].y][j-1],f[0][x][j]+=f[0][c[i].y][j-1];
}
void Dfs(int x=1)
{
	if(x!=1) for(int i=1;i<d[x];++i)
	  f[1][x][i]=f[1][fa[x]][i-1]+f[0][fa[x]][i-1]-(i>1?f[0][x][i-2]:1),ans[x]+=1ll*f[1][x][i]*f[0][x][i];
	for(int i=h[x];i;i=c[i].x)
	  if(c[i].y!=fa[x]) Dfs(c[i].y);
}
int main()
{
	n=read();
	for(int i=1;i<n;++i,add());
	dfs(),Dfs();
	for(int i=1;i<=n;++i)
	  printf("%lld ",ans[i]+1);
	return 0;
}

题目