猫树
听说叫猫树是因为发明者$immortalCO$(猫锟)觉得猫是一种很可爱的生物qwq
一道题:
给定一个长度为$n$的序列,每次询问查询区间最大子段和
线段树随便艹啊……
复杂度是$O(n+qlogn)$(建树+查询)
这时候毒瘤出题人就说了:诶你这复杂度不优秀,要求查询不要带$log$

这时候一种可爱的数据结构就蹦出来解决ta啦,也就是猫树,复杂度是$O(nlogn+q)$($O(nlogn)$预处理,$O(1)$查询)
猫树主要用来解决区间查询某种支持结合律和快速合并的信息,并且没有修改操作
想想线段树怎么合并区间信息的
区间$[l,r]$信息是$[l,mid]$和$[mid+1,r]$的信息结合起来
考虑处理$mid$向前和向后的答案
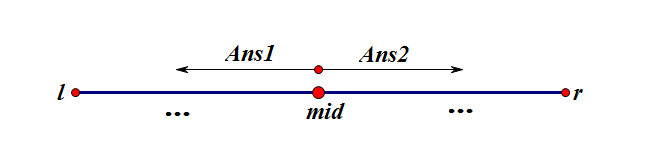
设$l$和$r$在线段树上最后在一个区间(儿子区间中分开)的节点为$A$,显然$A$为$l,r$的$lca$
如果能快速找到$A$,就可以直接合$并[l,mid]$和$[mid+1,r]$的答案
既然是lca那么求一下树上lca就好啦
如果$i$的儿子节点为$2i$和$2i+1$,发现任意同深度的两个节点,ta们的$lca$就是ta们节点标号二进制表示的$lcp$(分开位置前面肯定是一样的祖先)
两个数$a,b$二进制$lcp$为$a»\log_{2}^{a\oplus b}$
这样就可以$O(1)$查询了qwq
上面例题的部分代码:
struct Cat_Tree{
int sum1[21][MAX],sum2[21][MAX];
void build(int l=1,int r=qaq,int k=1,int d=1)//qaq是最底层填满了的大小,k为编号,d为深度
{
if(l==r) return void(pos[l]=k);
int sum,_sum;
sum1[d][mid]=sum2[d][mid]=sum=_sum=a[mid],_sum=min(_sum,0);
for(int i=mid-1;i>=l;--i)
sum1[d][i]=max(sum1[d][i+1],sum+=a[i]),sum2[d][i]=max(sum2[d][i+1],sum-_sum),_sum=min(_sum,sum);
sum1[d][mid+1]=sum2[d][mid+1]=sum=_sum=a[mid+1],_sum=min(_sum,0);
for(int i=mid+2;i<=r;++i)
sum1[d][i]=max(sum1[d][i-1],sum+=a[i]),sum2[d][i]=max(sum2[d][i-1],sum-_sum),_sum=min(_sum,sum);
build(l,mid,tl,d+1),build(mid+1,r,tr,d+1);
}
int ask(int l,int r)
{
if(l==r) return a[l];
int qwq=Log[pos[l]]-Log[pos[l]^pos[r]];
return max(sum2[qwq][l]+sum2[qwq][r],max(sum1[qwq][l],sum1[qwq][r]));
}
}Tree;
单调对联
恭喜您发现彩蛋!
在$2018$年的初春,一名叫做$zyf$的julao经过呕心沥血的研究,终于发明了单调对联这一划时代的数据结构
$Q:$ta能解决什么问题呢?
经过多次尝试,我们惊讶的发现,在面对任意一个没有询问的序列问题时,这种数据结构都能做到$O(1)$的优秀时间复杂度!而空间复杂度也是极小的!
但是遗憾的是,由于$zyf$先生的码风过于毒瘤,现在我们还没能做到研究透彻ta是如何处理能达到如此高效的复杂度,也许这就是凡人无法理解的智慧吧
好消息是应多方响应,$zyf$已经同意将单调对联加入百度百科,美其名曰数组
希望能早日理解$zyf$先生的智慧,想必这场$OI$界的巨大变革能使数据结构能有更大的发展!
不行我编不下去了

