题目
题目大意
多组数据
给定一个无向图,问是否存在奇环/偶环
Sample Input
3
1 0
3 3
1 2
2 3
3 1
4 4
1 2
2 3
3 4
4 1
Sample Output
NO
NO
YES
NO
NO
YES
题解
判断奇环,只要判断这个图是否是一个二分图即可
判断偶环,建立$dfs$树的时候,如果遇到返祖边,两个点之间的边数为奇数说明存在偶环
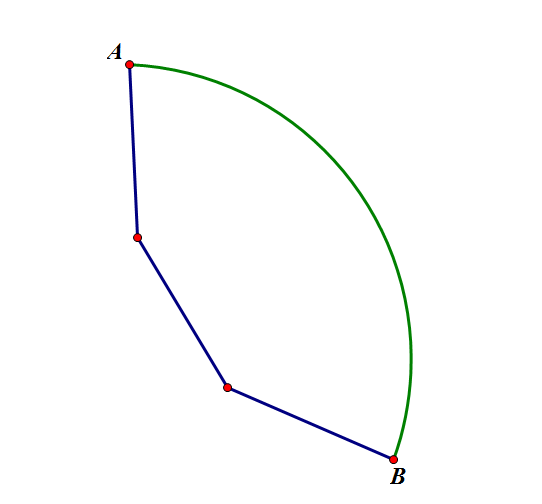
但是还可能有两个奇环拼成一个偶环的情况,如图:
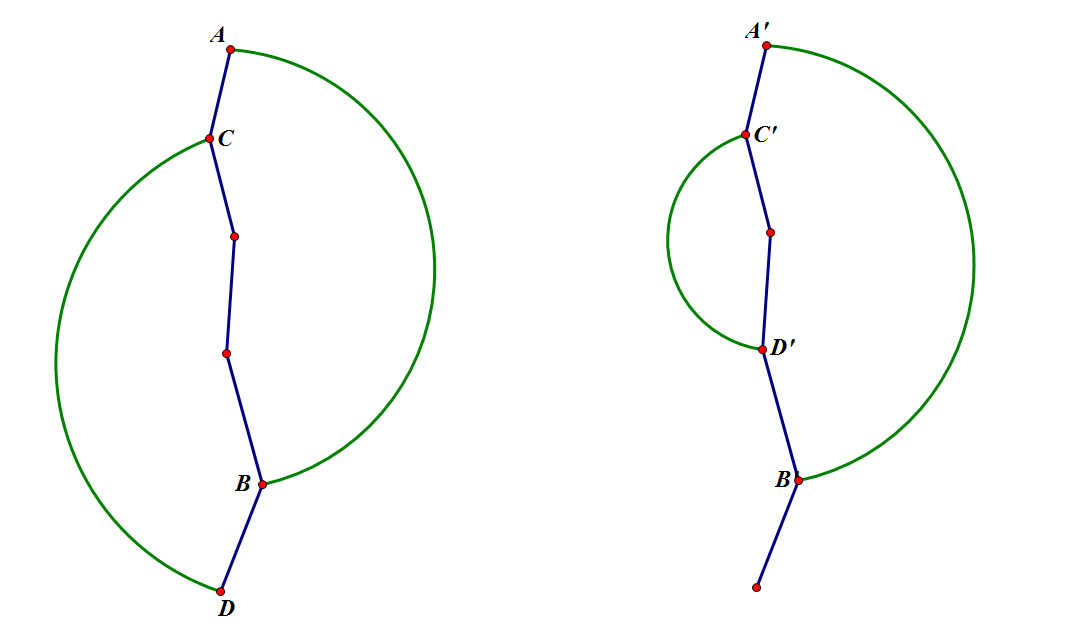
发现如果返祖边到的点在某个奇环之内,ta也存在偶环
所以每次找到返祖边都把两点之间的点标记一下判断即可
代码
# include<bits/stdc++.h>
using namespace std;
const int MAX=3e5+5;
struct p{
int x,y;
}c[MAX<<1];
int n,m,num;
int h[MAX],f[MAX],d[MAX],col[MAX];
bool fl,fl1;
bool _col[MAX];
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
void add()
{
int x=read(),y=read();
c[++num]=(p){h[x],y},h[x]=num;
c[++num]=(p){h[y],x},h[y]=num;
}
void dfs(int x,int fa=0)
{
d[x]=d[fa]+1,col[x]=col[fa]^1,f[x]=fa;
for(int i=h[x];i;i=c[i].x)
if(c[i].y!=fa)
{
if(col[c[i].y]!=-1)
{
if(col[c[i].y]==col[x])
{
fl1=1;
for(int l=x;l!=c[i].y&&l;l=f[l])
{
if(_col[l]) fl=1;
_col[l]=1;
if(fl) break;
}
}
else fl=1;
}
else dfs(c[i].y,x);
if(fl&&fl1) break;
}
}
int main()
{
int T=read();
do{
n=read(),m=read();
memset(h,0,sizeof(h));
memset(_col,0,sizeof(_col));
memset(col,-1,sizeof(col));
memset(d,0,sizeof(d));
num=fl=fl1=col[0]=0;
for(int i=1;i<=m;++i,add());
for(int i=1;i<=n;++i)
if(col[i]==-1) dfs(i);
fl1?printf("YES\n"):printf("NO\n");
fl?printf("YES\n"):printf("NO\n");
}while(--T);
return 0;
}

