题目
题目大意
给定一个带权无向图
对于每条边，求其他边不变时这条边能出现在这个图的每一个最小生成树上，这条边满足条件的最大权值是多少
Examples
input
4 4
1 2 2
2 3 2
3 4 2
4 1 3
output
2 2 2 1
input
4 3
1 2 2
2 3 2
3 4 2
output
-1 -1 -1
题解
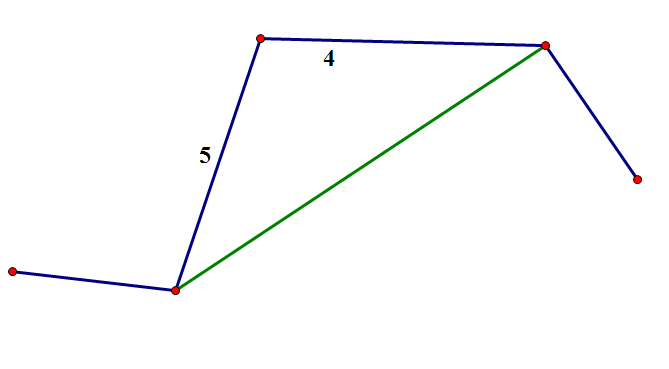如图，绿边表示非树边，蓝边表示树边，很容易看出来一条非树边的答案应该是ta两端之间树边的最大值$-1$，这样ta才能不被替换掉
树边的答案需要非树边来更新
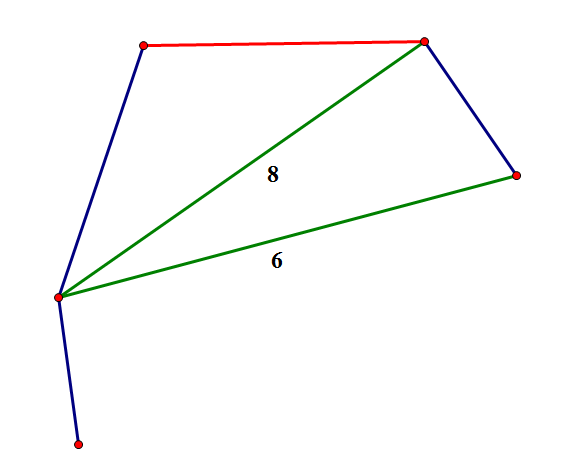如图，红边表示要更新的树边，因为非树边一定不小于树边，树边答案应该为非树边权值$-1$，即保证最小生成树只能选ta这条边
所以树边答案为两端包含ta的非树边的最小值$-1$
代码
# include<bits/stdc++.h>
using namespace std;
const int MAX=2e5+1;
struct p{
int x,y,dis,id;
bool operator< (const p &a)
const{
return dis<a.dis;
}
}c[MAX],cc[MAX<<1];
int n,m,num;
int d[MAX],h[MAX],fa[MAX],Ans[MAX],ID[MAX];
int f[MAX][19],maxn[MAX][19];
bool use[MAX];
int read()
{
int x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
void dfs(int x,int fa=0)
{
d[x]=d[fa]+1,f[x][0]=fa;
for(int i=h[x];i;i=cc[i].x)
if(cc[i].y!=fa) maxn[cc[i].y][0]=cc[i].dis,ID[cc[i].y]=cc[i].id,dfs(cc[i].y,x);
}
int LCA(int x,int y)
{
if(d[x]>d[y]) swap(x,y);
int D=d[y]-d[x];
for(int i=0;(1<<i)<=D;++i)
if((1<<i)&D) y=f[y][i];
if(x==y) return x;
for(int i=18;i>=0;--i)
if(f[y][i]!=f[x][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
void add(int x,int y,int dis,int id)
{
cc[++num]=(p){h[x],y,dis,id},h[x]=num;
cc[++num]=(p){h[y],x,dis,id},h[y]=num;
}
void init()
{
for(int i=1;i<=18;++i)
for(int j=1;j<=n;++j)
f[j][i]=f[f[j][i-1]][i-1],maxn[j][i]=max(maxn[j][i-1],maxn[f[j][i-1]][i-1]);
}
int GET_DIS(int x,int y)
{
int ans=0;
for(int i=18;i>=0;--i)
if(d[f[x][i]]>=d[y]) ans=max(ans,maxn[x][i]),x=f[x][i];
return ans;
}
int find(int x)
{
if(fa[x]!=x) fa[x]=find(fa[x]);
return fa[x];
}
void change(int x,int y,int dis)
{
int qwq=find(x);
while(d[qwq]>d[y])
Ans[ID[qwq]]=min(Ans[ID[qwq]],dis),fa[qwq]=find(f[qwq][0]),qwq=fa[qwq];
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;++i)
fa[i]=i;
for(int i=1;i<=m;++i)
c[i].x=read(),c[i].y=read(),c[i].dis=read(),c[i].id=i,Ans[i]=2e9;
sort(c+1,c+1+m);
for(int i=1,L=0;i<=m;++i)
{
if(L==n-1) break;
int r1=find(c[i].x),r2=find(c[i].y);
if(r1==r2) continue;
fa[r1]=r2,add(c[i].x,c[i].y,c[i].dis,c[i].id),use[i]=1;
}
for(int i=1;i<=n;++i)
fa[i]=i;
dfs(1),init();
for(int i=1,lca;i<=m;++i)
if(!use[i])
lca=LCA(c[i].x,c[i].y),Ans[c[i].id]=max(GET_DIS(c[i].x,lca),GET_DIS(c[i].y,lca))-1,change(c[i].x,lca,c[i].dis-1),change(c[i].y,lca,c[i].dis-1);
for(int i=1;i<=m;++i)
printf("%d ",Ans[i]==2e9?-1:Ans[i]);
return 0;
}
