题目
题意大意
给定3个点的坐标，求以这3个点为顶点的正多边形的最小面积
满足条件的正多边形的边数不超过100，忽略不超过1e-6的精度误差
输入输出样例
输入样例#1：
0.000000 0.000000
1.000000 1.000000
0.000000 1.000000
输出样例#1：
1.00000000
题解
因为一条边对应的圆心角肯定得被给定三个顶点之间的圆心角整除（不然放不开），并且一条边对应的圆心角越大多边形面积就越小（类比正方形和圆）
边数就是$\frac{2\pi}{\gcd}$，所以题目可以通过求出三个圆心角的最大公约数从而求出最小多边形的面积
先不管怎么求浮点数的最大公约数
假设给定的三个点如图所示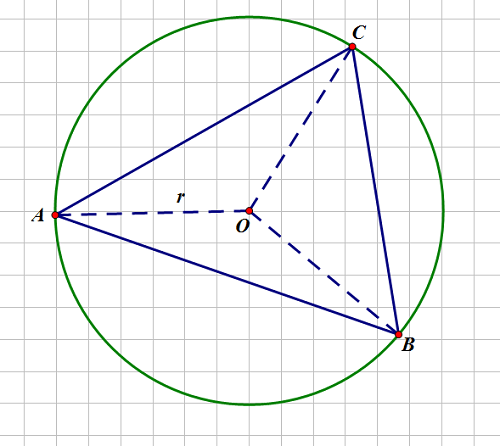
通过$A,B,C$的坐标可以求出边$a,b,c$，根据海伦公式$S=\sqrt{P(P-a)(P-b)(P-c)}(P=\frac{a+b+c}{2})$可以求出三角形面积$S$
因为$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2r,S=\frac{bcsinA}{2}$
可得$r=\frac{abc}{4S}$
这样通过余弦定理$cosA’=\frac{2r^2-a^2}{2r^2}=1-\frac{a^2}{2r^2}$就可以求出每个圆心角了
求出圆心角就可以求最大公约数了，浮点数的最大公约数求法跟整数差不多，但是要控制精度
题目中有个条件看似无用？
保证在最佳答案中多边形角的数目不大于100
通过这个可以发现多边形圆心角不小于$0.01\times 2\pi\approx 0.06$，所以求$\gcd$过程中小于$0.06$的值都认成0就行了
似乎出现本机WA提交AC的情况？QAQ
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<cmath>
using namespace std;
const double fs=6e-2,Pi=acos(-1.0);
struct point{
double x,y;
}p[4];
double a,b,c,r,S,C,P,C1,A1,B1,R1,Ans;
double s(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double gcd(double a,double b)
{
return (fabs(b)>fs)?gcd(b,fmod(a,b)):a;
}
int main()
{
for(int i=1;i<=3;++i)
scanf("%lf%lf",&p[i].x,&p[i].y);
a=s(p[1],p[2]),b=s(p[2],p[3]),c=s(p[1],p[3]),P=(a+b+c)/2;
S=sqrt(P*(P-a)*(P-b)*(P-c)),r=a*b*c/(4*S);
C1=acos(1-c*c/(2*r*r)),A1=acos(1-a*a/(2*r*r)),B1=2*Pi-A1-C1;
R1=gcd(A1,gcd(B1,C1));
return printf("%.6lf",(Pi*r*r*sin(R1))/R1),0;
}
