题目
题目大意
给你一个$L$，让你用最多$20$个点，$30$条边来构造一个图，满足编号小的连向编号大的，$1$到$N$有$L$条长度不同的路径，ta们的长度为$0$到$L-1$
Constraints
- $2≤L≤10^6$
- $L$ is an integer.
Sample Input 1
4
Sample Output 1
8 10
1 2 0
2 3 0
3 4 0
1 5 0
2 6 0
3 7 0
4 8 0
5 6 1
6 7 1
7 8 1
Sample Input 2
5
Sample Output 2
5 7
1 2 0
2 3 1
3 4 0
4 5 0
2 4 0
1 3 3
3 5 1
题解
可以yy一下，经过点与点之间连两条边，一条边长为$2$的次幂，一条边为$0$
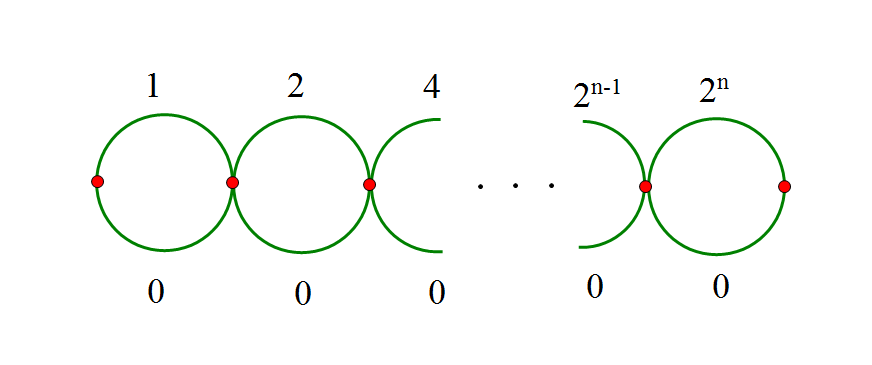
这个$n$肯定是$2$进制下$L$的最高位$-1$，这样的图可以构成$2^n$条路径，即路径长度$L$最高位的位置不为$1$的情况
现在处理路径长度$L$最高位的位置为$1$的情况，emmmm举个例子是不是比较直观？
假设$L=43$，即$101011$
那首先有这个图：
剩下的部分也$2$进制处理，发现$32$和以后的数无法出现
长度为$32$的边与长度为$4$的边相连的点相连，如图：
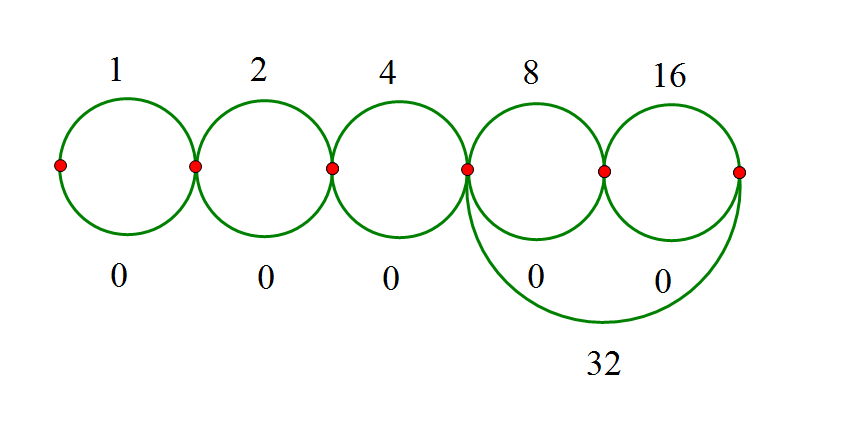这样最大能构成的数为$39$
然后长度为$40$的边与长度为$2$的边相连的点相连，如图：
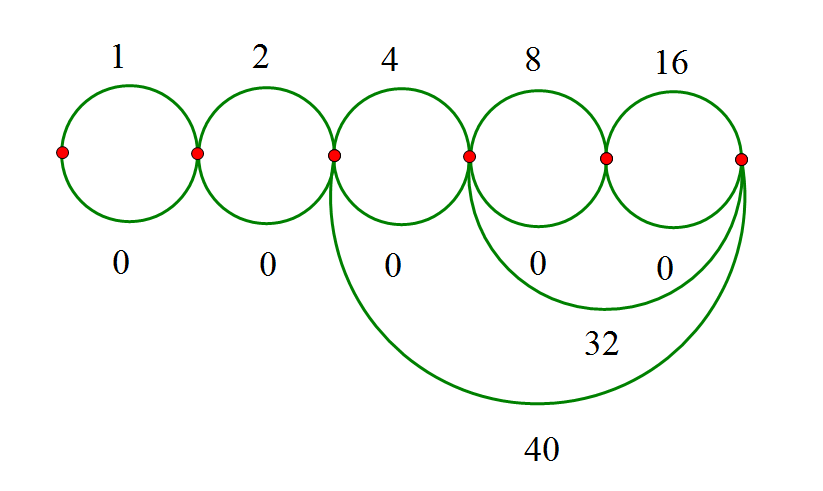这样最大能构成的数为$43$，满足题意的图就构造出来了
所以每次选相加不超过$L$且结果最大的点相连，然后找构成上界继续
代码
# include<iostream>
# include<cstdio>
# include<cstring>
using namespace std;
const int MAX=101;
struct p{
int x,y,dis;
}c[MAX];
int L,num,h;
void add(int x,int y,int dis)
{
c[++num]=(p){x,y,dis};
}
int main()
{
scanf("%d",&L);
for(int i=20;i>=0;--i)
if((1<<i)<=L)
{
h=i;
break;
}
for(int i=1;i<h;++i)
add(i,i+1,0),add(i,i+1,1<<i-1);
add(h,20,0),add(h,20,1<<h-1);
int G=1<<h;
while(G<L)
{
int tt=1;
while((1<<tt)<=L-G) ++tt;
add(tt,20,G),G|=(1<<tt-1);
}
printf("20 %d\n",num);
for(int i=1;i<=num;++i)
printf("%d %d %d\n",c[i].x,c[i].y,c[i].dis);
return 0;
}
