K-D Tree是种非常鬼畜的数据结构…
跟平衡树一样，$K-D$ $Tree$是一棵二叉树，不同的是，$K-D$ $Tree$的每一层构建左右儿子的指标都不同，于是$K-D$ $Tree$的画风就十分鬼畜QAQ
先看一道简单题：
N*N的棋盘，要求支持单点修改和区间求和，内存限制20M
这不是树套树裸题吗暴力数据结构大法好
但是$N\le 500000$，树套树最差情况下需要$4000G$（噗），空间爆炸
emmmm可以用$CDQ$分治搞
那要是强制在线就不能搞了
这时候就需要$K-D$ $Tree$了，每个修改操作可以看成加入一个点，注意每一层要换一个指标，这里指标就是横纵坐标
然后就跟平衡树的加入操作一样了
void add(int &k,int x,bool D)//k是当前点编号，x为加入点编号，D为指标，D=0指标为横坐标，否则为纵坐标
{
if(!k)
{
k=x;
return;
}
if(s[x].d[D]<=s[k].d[D]) add(tl,x,D^1);//向左走，注意换指标
else add(tr,x,D^1);//向右走
pus(k),look(k,D);//pus即子节点上推，look目前用不到
}
举个栗子：现在加入了6个点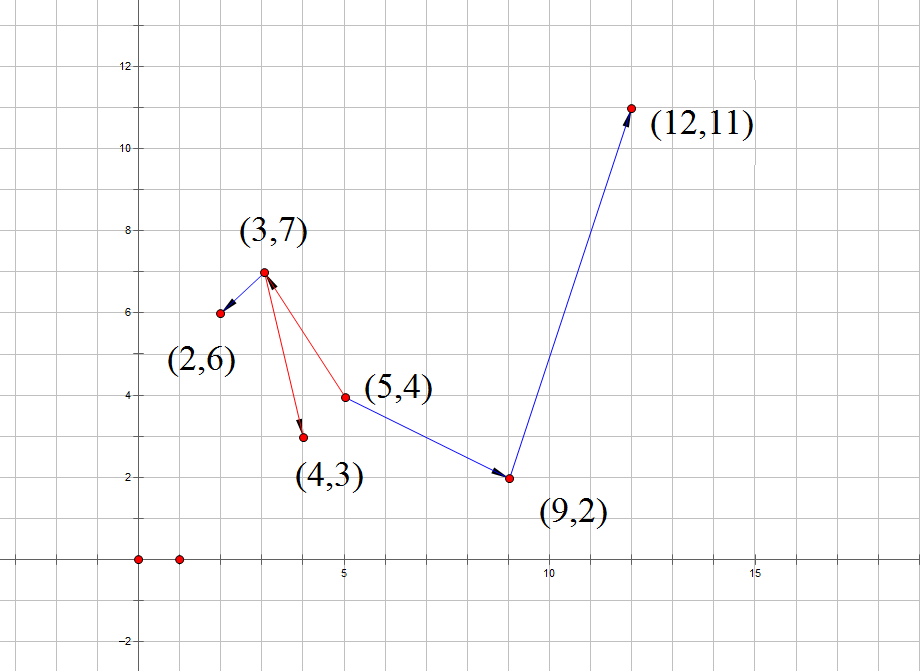
红边连接表示左儿子，蓝边连接表示右儿子，加入顺序是$(5,4),(3,7),(9,2),(2,6),(4,3),(12,11)$，映射一下就成了这张鬼畜的图
每个节点维护9个值：子树横坐标最大值、最小值，子树纵坐标最大值、最小值，这个节点图中对应的点的横纵坐标，左、右儿子编号和这个范围内的点值和
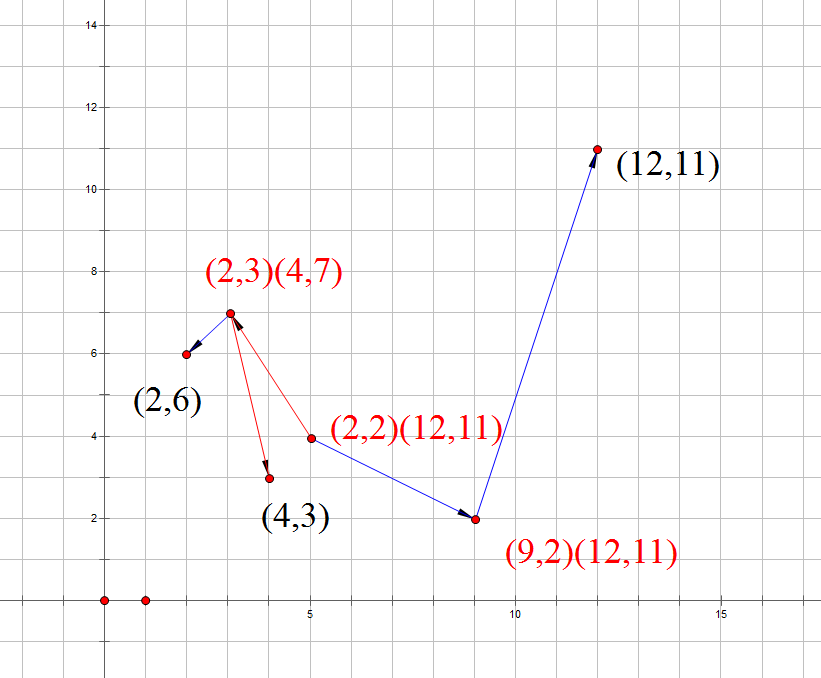
可以看出，每个节点维护的最大最小值相当于维护一个矩形区域，如图：
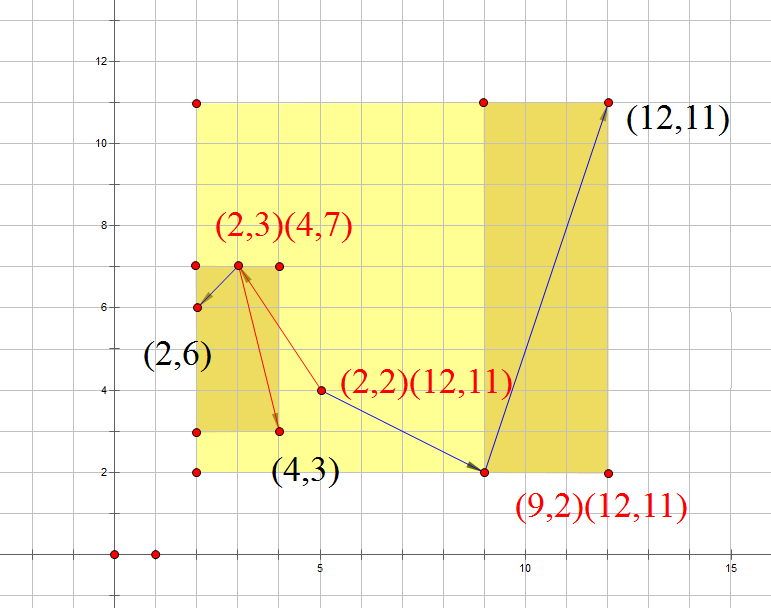
黄颜色部分为每个节点维护区域，当遇到一个查询时，如图，褐色部分为查询区域：
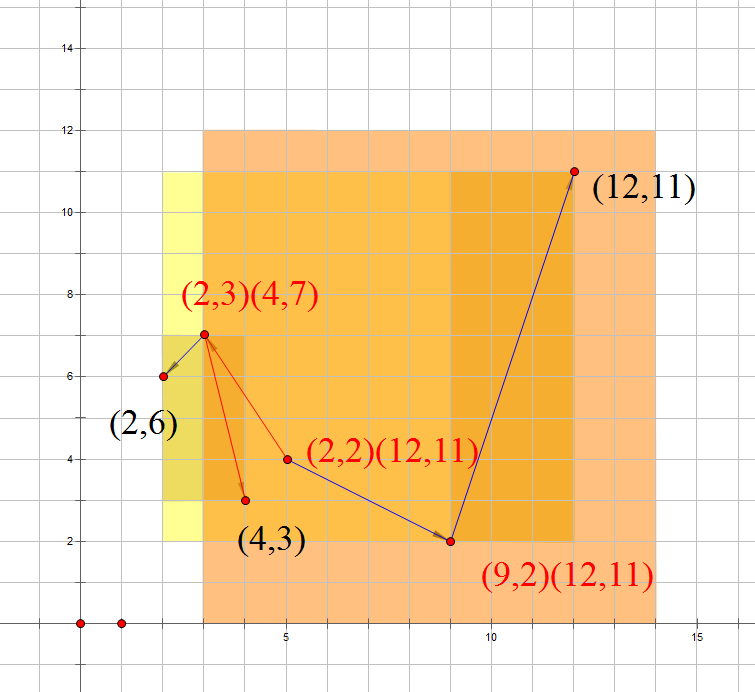
从跟开始遍历，如果当前节点维护的矩阵在查询范围内，就返回这个节点维护的点权和，如果完全不在范围内就返回$0$，如果部分在范围内就继续遍历两个儿子是不是非常有道理
总而言之，$K-D$ $Tree$的操作分为这么几个步骤：
-
加入点，建出一棵二叉树，每个节点维护子树信息
-
应对询问，进行修改或查询
-
查询时根据估价函数进行判断，上述栗子中估价函数就是判断查询矩阵和节点维护矩阵的关系，估价函数设计的好坏影响$K-D$ $Tree$的时间复杂度
$K-D$ $Tree$还能解决$k$近邻搜索问题，比如：
n维空间，给定一堆点，每次查询到某个坐标的欧几里得距离（只要是跟每个维度有关的距离就行，这里是欧几里得距离）第$k$大的点
$n$维空间表示指标有$n$个，每层依次选择就行了，类比二维空间（即棋盘）每个节点维护的还是一个“矩形”
先想一下如果要查询最大距离该怎么办
那么我们应该让树遍历的当前节点远离查询坐标
所以设计估价函数计算一下查询坐标到左右儿子维护的“矩形”边界的最小欧几里得距离，进行比较
LL GET_DIS(int k)//估价函数
{
LL sum=0;//到编号为k的点维护“矩形”边界的距离
if(!k) return 1e18;//没有这个点就不能继续遍历
for(int i=0;i<K;++i)//计算距离
if(s[k].maxn[i]<S.d[i]) sum+=1ll*(S.d[i]-s[k].maxn[i])*(S.d[i]-s[k].maxn[i]);
else if(s[k].minn[i]>S.d[i]) sum+=1ll*(s[k].minn[i]-S.d[i])*(s[k].minn[i]-S.d[i]);
return sum;//返回距离
}
如果左右儿子距离都小于已有答案，说明将要遍历的子树不会给答案作出贡献，直接退出就行了
否则，如果左儿子距离大于右儿子距离，就往左儿子走，否则就往右儿子走，到一个节点就与ta对应的图中的点计算距离并更新答案
查找最近点反着来做就行了
这是最大距离的查询，第k大距离怎么办呢？
维护个堆就行了
这道题就是查找最近点
但是你估摸着码完了会极有可能TLE一个点
即便有了估价函数，但是若是遍历的点的子树极其深，就会增加递归层数
这时候就需要替罪羊式重构一下子树了
加入节点的时候，用$look$函数检查左右子树大小是否有一个大于全部子树的大小乘上一个参数（一般是$0.75$）
如果有，就把全部子树遍历一遍，记录下每个节点（可以垃圾回收减少内存，用个栈记录下），然后重新构造
int GET_POINT()//垃圾回收
{
if(top) return st[top--];
return ++tot;
}
void build(int l,int r,bool d)//d是指标，tl是左儿子，tr是右儿子（宏定义过了QAQ）
{
if(l>r) return 0;
D=d;
int k=GET_POINT(),mid=(l+r>>1);//垃圾回收减少内存
nth_element(s1+l,s1+mid,s1+1+r);//先建树，这里二分一下点序列，nth_element可以让s1[mid]成为序列中间位置，这里按照这一层的指标找mid
s[k]=s1[mid],s[k].siz=1;//s即建出来的真正的树，s1是重构前的点序列
tl=build(l,mid-1,d^1),tr=build(mid+1,r,d^1);
return pus(k),k;//pus上推节点信息
}
void dfs(int k,int siz)//遍历子树
{
if(tl) dfs(tl,siz);
s1[siz+s[tl].siz]=s[k],st[++top]=k;
if(tr) dfs(tr,siz+s[tl].siz+1);
}
void look(int &k,bool D)//k为当前点，D为指标
{
if(s[tl].siz>alpha*s[k].siz||s[tr].siz>alpha*s[k].siz)//alpha为0.75
dfs(k,1),k=build(1,s[k].siz,D);//重构
}
几道练手题：
