题目
题目描述
曾经发明了自动刷题机的发明家 SHTSC 又公开了他的新发明:脑洞治疗仪——一种可以治疗他因为发明而日益增大的脑洞的神秘装置。
为了简单起见,我们将大脑视作一个 01 序列。$1$代表这个位置的脑组织正常工作,$0$代表这是一块脑洞。
1 0 1 0 0 0 1 1 1 0
脑洞治疗仪修补某一块脑洞的基本工作原理就是将另一块连续区域挖出,将其中正常工作的脑组织填补在这块脑洞中。(所以脑洞治疗仪是脑洞的治疗仪?)
例如,用上面第$8$号位置到第$10$号位置去修补第$1$号位置到第$4$号位置的脑洞,我们就会得到:
1 1 1 1 0 0 1 0 0 0
如果再用第$1$号位置到第$4$号位置去修补第$8$号位置到第$10$号位置:
0 0 0 0 0 0 1 1 1 1
这是因为脑洞治疗仪会把多余出来的脑组织直接扔掉。
如果再用第$7$号位置到第$10$号位置去填补第$1$号位置到第$6$号位置:
1 1 1 1 0 0 0 0 0 0
这是因为如果新脑洞挖出来的脑组织不够多,脑洞治疗仪仅会尽量填补位置比较靠前的脑洞。
假定初始时 SHTSC 并没有脑洞,给出一些挖脑洞和脑洞治疗的操作序列,你需要即时回答 SHTSC 的问题:在大脑某个区间中最大的连续脑洞区域有多大。
输入输出格式
输入格式:
第一行两个整数$n,m$,表示 SHTSC 的大脑可分为从$1$到$n$编号的$n$个连续区域,有$m$个操作。
以下$m$行每行是下列三种格式之一:
$0 l r$:SHTSC 挖了一个范围为$[l,r]$的脑洞。
$1 l_0 r_0 l_1 r_1$:SHTSC 进行了一次脑洞治疗,用从$l_0$到$r_0$的脑组织修补$l_1$到$r_1$的脑洞。
$2 l r$:SHTSC 询问$[l,r]$区间内最大的脑洞有多大。
上述区间均在$[1,n]$范围内。
输出格式:
对于每个询问,输出一行一个整数,表示询问区间内最大连续脑洞区域有多大。
输入输出样例
输入样例#1:
10 10
0 2 2
0 4 6
0 10 10
2 1 10
1 8 10 1 4
2 1 10
1 1 4 8 10
2 1 10
1 7 10 1 6
2 1 10
输出样例#1:
3 3 6 6
说明
对于20%的数据,$n,m\leq 100$;
对于50%的数据,$n,m\leq 20000$;
对于100%的数据,$n,m\leq 200000$。
题解
线段树裸题,维护最大连续子段
操作只有区间覆盖(全变为$0$)和一个区间补全(姑且这么命名)
区间覆盖好说,一个标记就行了
区间补全怎么搞呢?
可以在给定的区间里找出连续为$0$的一段,并且你现在有的脑组织可以填满ta
这样就又是区间覆盖(全变为$1$)了
要是脑组织不够,就继续二分直到找到可以填满的区间
如图: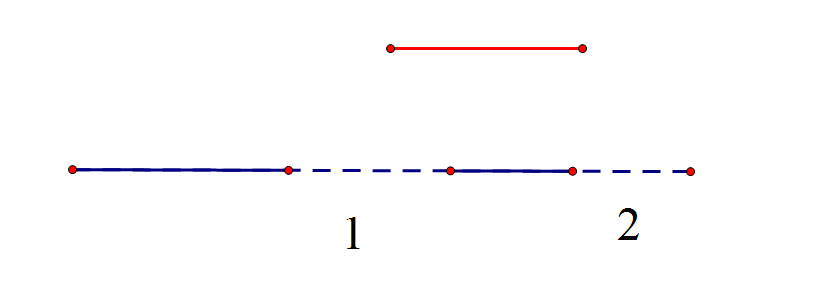
红色线段是有的脑组织,蓝色虚线部分是脑洞
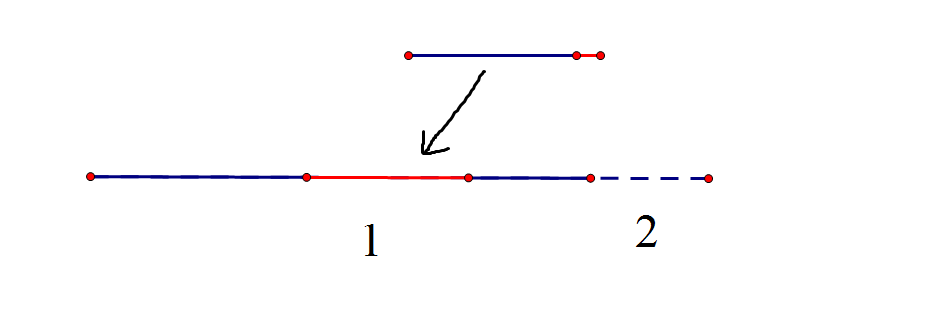
把红色部分填进脑洞$1$
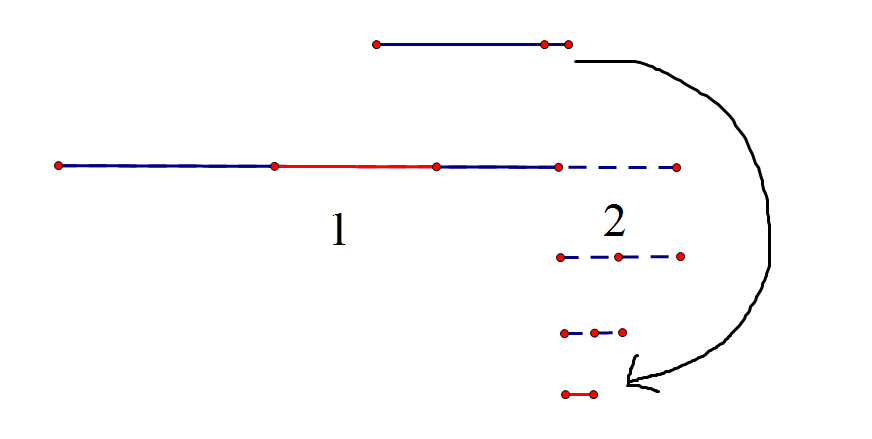
这时红色剩余部分不够填充脑洞$2$了,于是二分脑洞$2$直到找到可以填充的部分
这样加上一些优化时间复杂度大概是$O(n\log n)$多一点?我也不会算
反正开$O2$跑的挺快qwq
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<algorithm>
# define tl (k<<1)
# define tr (k<<1|1)
# define mid (l+r>>1)
using namespace std;
const int MAX=2e5+1;
struct p{
int Sum,l,r,sum,lazy;
p(){lazy=-1;}
}s[MAX<<2];
int n,m,tot,TOT;
int read()
{
int x=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
p pus(int dis,p a,p b,int l,int r)
{
p c;
c.l=c.r=c.sum=c.Sum=0,c.lazy=dis;
c.Sum=a.Sum+b.Sum;
c.l=a.l,c.r=b.r;
if(a.l==mid-l+1) c.l+=b.l;
if(b.r==r-mid) c.r+=a.r;
c.sum=a.r+b.l;
c.sum=max(c.sum,max(a.sum,b.sum));
c.sum=max(c.l,max(c.r,c.sum));
return c;
}
void down(int l,int r,int k)
{
int dis=s[k].lazy;
s[k].lazy=-1;
if(dis==-1) return;
s[tl].Sum=dis*(mid-l+1),s[tl].sum=s[tl].l=s[tl].r=(dis==0)*(mid-l+1),s[tl].lazy=dis;
s[tr].Sum=dis*(r-mid),s[tr].sum=s[tr].l=s[tr].r=(dis==0)*(r-mid),s[tr].lazy=dis;
}
void change1(int l,int r,int k,int L,int R)
{
if(l==L&&r==R)
{
s[k].Sum=0,s[k].sum=s[k].l=s[k].r=r-l+1,s[k].lazy=0;
return;
}
down(l,r,k);
if(R<=mid) change1(l,mid,tl,L,R);
else if(L>mid) change1(mid+1,r,tr,L,R);
else change1(l,mid,tl,L,mid),change1(mid+1,r,tr,mid+1,R);
s[k]=pus(s[k].lazy,s[tl],s[tr],l,r);
}
void change3(int l,int r,int k)
{
if(!TOT) return;
if(s[k].Sum==r-l+1) return;
if(!s[k].Sum&&TOT>=r-l+1)
{
s[k].Sum=r-l+1,s[k].sum=s[k].l=s[k].r=0,s[k].lazy=1;
TOT-=r-l+1,tot+=r-l+1;
return;
}
if(l>=r) return;
down(l,r,k);
change3(l,mid,tl),change3(mid+1,r,tr);
s[k]=pus(s[k].lazy,s[tl],s[tr],l,r);
}
void change2(int l,int r,int k,int L,int R,int dis)
{
if(tot>=dis) return;
if(l==L&&r==R)
{
TOT=dis-tot,change3(l,r,k);
return;
}
down(l,r,k);
if(R<=mid) change2(l,mid,tl,L,R,dis);
else if(L>mid) change2(mid+1,r,tr,L,R,dis);
else change2(l,mid,tl,L,mid,dis),change2(mid+1,r,tr,mid+1,R,dis);
s[k]=pus(s[k].lazy,s[tl],s[tr],l,r);
}
int ask1(int l,int r,int k,int L,int R)
{
if(l==L&&r==R) return s[k].Sum;
down(l,r,k);
if(R<=mid) return ask1(l,mid,tl,L,R);
if(L>mid) return ask1(mid+1,r,tr,L,R);
return ask1(l,mid,tl,L,mid)+ask1(mid+1,r,tr,mid+1,R);
}
p ask2(int l,int r,int k,int L,int R)
{
if(l==L&&r==R) return s[k];
down(l,r,k);
if(R<=mid) return ask2(l,mid,tl,L,R);
if(L>mid) return ask2(mid+1,r,tr,L,R);
p LL=ask2(l,mid,tl,L,mid),RR=ask2(mid+1,r,tr,mid+1,R);
return pus(-1,LL,RR,l,r);
}
int Ask(int l,int r)
{
int ans=ask1(1,n,1,l,r);
change1(1,n,1,l,r);
return ans;
}
int main()
{
n=read(),m=read();
s[1].lazy=1,s[1].Sum=n;
for(int i=1;i<=m;++i)
{
int op=read(),l=read(),r=read(),l1,r1;
if(!op) change1(1,n,1,l,r);
else if(op==1)
{
l1=read(),r1=read();
int dis=Ask(l,r);
if(dis) tot=TOT=0,change2(1,n,1,l1,r1,dis);
}
else if(op==2) printf("%d\n",ask2(1,n,1,l,r).sum);
}
return 0;
}

