[FJOI2007]轮状病毒

题目

题目描述

轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个n轮状基由圆环上n个不同的基原子和圆心的一个核原子构成。2个原子之间的边表示这2个原子之间的信息通道，如图1。

n轮状病毒的产生规律是在n轮状基中删除若干边，使各原子之间有唯一一条信息通道。例如，共有16个不同的3轮状病毒，入图2所示。

给定n(N<=100)，编程计算有多少个不同的n轮状病毒。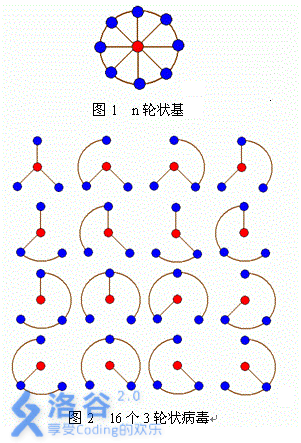

输入输出格式

输入格式：

第一行有1个正整数n。

输出格式：

将编程计算出的不同的n轮状病毒数输出

输入输出样例

输入样例#1：

输出样例#1：

题解

首先这题题意先看懂，就是求一个图中的最小生成树数量~~然后用矩阵树定理+高精瞎搞搞~~

然而作为一个啥也不会的菜鸡，怎么才能A掉这题呢？

这种题当然是找递推式子

所以打表找规律，自己写写画画数数~~然而n=4有45种情况233~~

然后你发现：

n	ans
0	0
1	1
2	5
3	16
4	45

可以愉快的发现$f_i=3*(f_{i-1}-f_{i-3})+f_{i-4}$

本来我想用矩乘的结果发现$n\leq 100$没必要

套上高精度，乱打一通这题就A啦

代码

# include<iostream>
# include<cstring>
# include<cstdio>
using namespace std;
int n;
int a[101],b[101];
string f[101];
string GET1(string A,string B)
{
  	int len;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
  	a[0]=A.length();
  	for(int i=1;i<=a[0];++i)
      a[i]=A[a[0]-i]-'0';
	b[0]=B.length();
  	for(int i=1;i<=b[0];++i)
      b[i]=B[b[0]-i]-'0';
  	len=(a[0]>b[0]?a[0]:b[0]);
  	for(int i=1;i<=len;++i)
      a[i]+=b[i],a[i+1]+=a[i]/10,a[i]%=10;   
  	++len;
  	while(!a[len]&&len>1) --len;
  	string ans="";
	for(int i=len;i>=1;--i)
      ans+=a[i]+48;
    return ans;
}
string GET2(string A,int B)
{
	int len;
  	memset(a,0,sizeof(a));
  	memset(b,0,sizeof(b));
  	a[0]=A.length();
  	for(int i=1;i<=a[0];++i)
      a[i]=A[a[0]-i]-'0';
  	for(int i=1;i<=a[0];++i)
      b[i]+=a[i]*B,b[i+1]+=b[i]/10,b[i]%=10;   
  	len=a[0]+2;
  	while(!b[len]&&len>1) --len;
  	string ans="";
  	for(int i=len;i>=1;--i)
  	  ans+=b[i]+48;
  	return ans;
}
string GET3(string A,string B)
{
	memset(a,0,sizeof(a));
  	memset(b,0,sizeof(b));
	a[0]=A.length();
  	for(int i=1;i<=a[0];++i)
      a[i]=A[a[0]-i]-'0';
  	b[0]=B.length();
  	for(int i=1;i<=b[0];++i)
      b[i]=B[b[0]-i]-'0';
    for(int i=1;i<=a[0];++i)
      {
	  	a[i]-=b[i];
       	if(a[i]<0) --a[i+1],a[i]+=10;
      }
    ++a[0];
    while(!a[a[0]]&&a[0]>1) --a[0];
    string ans="";
    for(int i=a[0];i>=1;--i)
      ans+=a[i]+48;
    return ans;
}
int main()
{
	scanf("%d",&n);
	f[0]="0",f[1]="1",f[2]="5",f[3]="16";
	for(int i=4;i<=n;++i)
	  f[i]=GET1(GET2(GET3(f[i-1],f[i-3]),3),f[i-4]);
	int len=f[n].length();
	for(int i=0;i<len;++i)
	  printf("%c",f[n][i]);
	return 0;
}

emmm我估计找规律+推式子+打高精考试就结束了233

所以还是乖乖去学矩阵树吧~~起码找规律不用一个一个画了~~

题目