题目
题目描述
Ayu 在七年前曾经收到过一个天使玩偶,当时她把它当作时间囊埋在了地下。而七年后 的今天,Ayu 却忘了她把天使玩偶埋在了哪里,所以她决定仅凭一点模糊的记忆来寻找它。
我们把 Ayu 生活的小镇看作一个二维平面坐标系,而 Ayu 会不定时地记起可能在某个点 (xmy) 埋下了天使玩偶;或者 Ayu 会询问你,假如她在 (x,y) ,那么她离近的天使玩偶可能埋下的地方有多远。
因为 Ayu 只会沿着平行坐标轴的方向来行动,所以在这个问题里我们定义两个点之间的距离为$dist(A,B)=\vert Ax-Bx\vert+\vert Ay-By\vert$。其中 Ax 表示点 A的横坐标,其余类似。
输入输出格式
输入格式:
第一行包含两个整数n和m ,在刚开始时,Ayu 已经知道有n个点可能埋着天使玩偶, 接下来 Ayu 要进行m 次操作
接下来n行,每行两个非负整数 (xi,yi),表示初始n个点的坐标。
再接下来m 行,每行三个非负整数 t,xi,yi。
如果t=1 ,则表示 Ayu 又回忆起了一个可能埋着玩偶的点 (xi,yi) 。
如果t=2 ,则表示 Ayu 询问如果她在点 (xi,yi) ,那么在已经回忆出来的点里,离她近的那个点有多远
输出格式:
对于每个t=2 的询问,在单独的一行内输出该询问的结果。
输入输出样例
输入样例#1:
2 3
1 1
2 3
2 1 2
1 3 3
2 4 2
输出样例#1:
1
2
说明
n,m<=300 000
xi,yi<=1 000 000
题解
可以把时间看成$1$个条件(初始点为$0$),坐标为$2$个条件
这样就成了一个三维偏序问题,似乎可以用$CDQ分治$搞了
然而曼哈顿距离带了个绝对值很烦人
所以分$4$种情况讨论
发现四种情况都可以看成是一个大矩阵套一个小矩阵
情况$1$: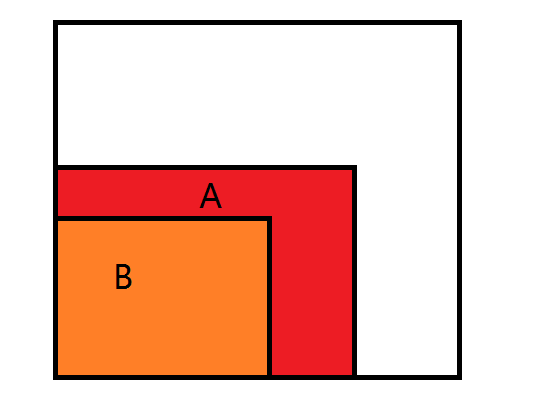
这是最简单的情况,直接找到二分左边的最大值减就行了
情况$2$: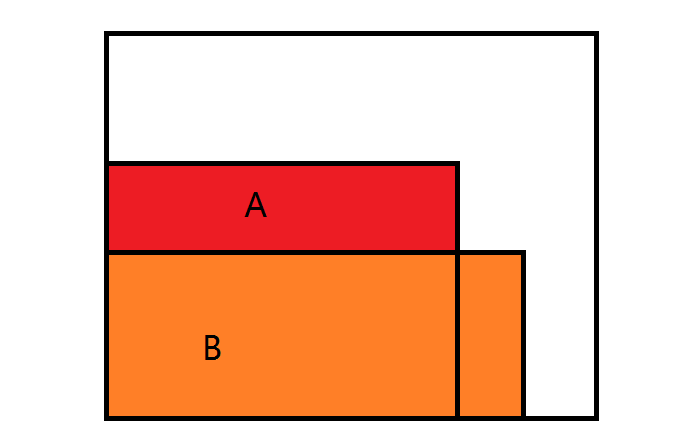
这种情况肯定不能直接减了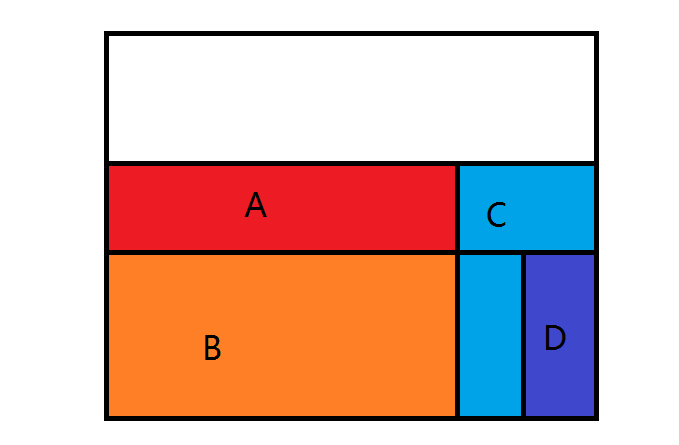
我们发现,用最大值减去$A,B$的$x$,可以得到两个新的矩阵$C,D$,而ta们满足条件$1$,而且答案不变
所以这么处理就行了
情况$3$、$4$同样处理
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<cstdlib>
# include<algorithm>
# define mid (l+r>>1)
using namespace std;
const int MAX=1e6+1;
int s[MAX];
int n,m,tot,maxn,maxx;
int ans[MAX];
int read()
{
int x=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
struct q{
int a,b,c,fl;
void Read()
{
b=read()+1,c=read()+1;
maxn=max(maxn,c),maxx=max(maxx,b);
}
}f[MAX],c[MAX];
bool cmp(q a,q b)
{
if(a.b!=b.b)
return a.b<b.b;
return a.a<b.a;
}
int lowbit(int x)
{
return x&(-x);
}
void change(int x,int dis)
{
for(int i=x;i<=maxn;i+=lowbit(i))
s[i]=max(s[i],dis);
}
int ask(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans=max(ans,s[i]);
return ans;
}
void cover(int x)
{
for(int i=x;i<=maxn;i+=lowbit(i))
s[i]=0;
}
void solve(int l,int r)
{
if(l==r) return;
int L1=l-1,L2=mid;
for(int i=l;i<=r;++i)
if(f[i].a<=mid) c[++L1]=f[i];
else c[++L2]=f[i];
memcpy(f+l,c+l,sizeof(q)*(r-l+1));
int L=l;
for(int i=mid+1;i<=r;++i)
if(f[i].fl==2)
{
for(;f[L].b<=f[i].b&&L<=mid;++L)
if(f[L].fl==1) change(f[L].c,f[L].c+f[L].b);
int tot1=ask(f[i].c);
if(tot1) ans[f[i].a]=min(ans[f[i].a],f[i].b+f[i].c-tot1);
}
for(int i=l;i<L;++i)
if(f[i].fl==1) cover(f[i].c);
solve(l,mid),solve(mid+1,r);
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;++i)
f[++tot].Read(),f[tot].fl=1,f[tot].a=tot;
for(int i=1;i<=m;++i)
f[++tot].fl=read(),f[tot].Read(),f[tot].a=tot;
++maxn,++maxx;
memset(ans,1,sizeof(ans));
sort(f+1,f+1+tot,cmp);
solve(1,tot);
for(int i=1;i<=tot;++i)
f[i].b=maxx-f[i].b;
sort(f+1,f+1+tot,cmp);
solve(1,tot);
for(int i=1;i<=tot;++i)
f[i].c=maxn-f[i].c;
sort(f+1,f+1+tot,cmp);
solve(1,tot);
for(int i=1;i<=tot;++i)
f[i].b=maxx-f[i].b;
sort(f+1,f+1+tot,cmp);
solve(1,tot);
for(int i=1;i<=tot;++i)
if(ans[i]<1e7) printf("%d\n",ans[i]);
return 0;
}

