题目
题目描述
从前有一个王国,这个王国的城堡是一个矩形,被分为M×N个方格。一些方格是墙,而另一些是空地。这个王国的国王在城堡里设了一些陷阱,每个陷阱占据一块空地。
一天,国王决定在城堡里布置守卫,他希望安排尽量多的守卫。守卫们都是经过严格训练的,所以一旦他们发现同行或同列中有人的话,他们立即向那人射击。因此,国王希望能够合理地布置守卫,使他们互相之间不能看见,这样他们就不可能互相射击了。守卫们只能被布置在空地上,不能被布置在陷阱或墙上,且一块空地只能布置一个守卫。如果两个守卫在同一行或同一列,并且他们之间没有墙的话,他们就能互相看见。(守卫就像象棋里的车一样)
你的任务是写一个程序,根据给定的城堡,计算最多可布置多少个守卫,并设计出布置的方案。
输入输出格式
输入格式:
第一行两个整数M和N(1≤M,N≤200),表示城堡的规模。
接下来M行N列的整数,描述的是城堡的地形。第i行j列的数用ai,j表示。
ai,j=0,表示方格[i,j]是一块空地;
ai,j=1,表示方格[i,j]是一个陷阱;
ai,j=2,表示方格[i,j]是墙。
输出格式:
第一行一个整数K,表示最多可布置K个守卫。
此后K行,每行两个整数xi和yi,描述一个守卫的位置。
输入输出样例
输入样例#1:
3 4
2 0 0 0
2 2 2 1
0 1 0 2
输出样例#1:
2
1 2
3 3
说明
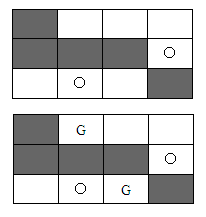
样例数据如图5-2(黑色方格为墙,白色方格为空地,圆圈为陷阱,G表示守卫)
题解
跟这道题思路一样
把每行、每列连续的一段缩成一个点并编号
然后可以选的位置行和列的编号相连,跑个最大流就行了
至于输出方案,把编号和行列对应一下就行了
代码
# include<iostream>
# include<cstdio>
# include<cstring>
# include<queue>
using namespace std;
const int MAX=401,inf=1e8,MAXX=(MAX*MAX<<1)+1,t=MAX*MAX<<1;
struct p{
int x,y,dis;
}c[MAXX<<1];
int n,m,tot,num,TOT;
int h[MAXX],d[MAXX],id[MAXX],id2[MAXX];
int colr[MAX][MAX],colc[MAX][MAX],a[MAX][MAX];
bool use[MAXX];
void add(int x,int y,int dis)
{
c[num]=(p){h[y],x,0};
h[y]=num++;
c[num]=(p){h[x],y,dis};
h[x]=num++;
}
bool bfs()
{
queue<int> qu;
qu.push(0);
memset(d,0,sizeof(d));
d[0]=1;
while(!qu.empty())
{
int tt=qu.front();
qu.pop();
for(int i=h[tt];i;i=c[i].x)
if(!d[c[i].y]&&c[i].dis)
{
d[c[i].y]=d[tt]+1;
qu.push(c[i].y);
}
}
return d[t];
}
int dfs(int x,int dix)
{
if(!dix||x==t) return dix;
int sum=0;
for(int i=h[x];i;i=c[i].x)
if(d[c[i].y]==d[x]+1&&c[i].dis)
{
int dis=dfs(c[i].y,min(dix,c[i].dis));
if(dis)
{
dix-=dis;
sum+=dis;
c[i].dis-=dis;
c[i^1].dis+=dis;
if(!dix) break;
}
}
if(!sum) d[x]=-1;
return sum;
}
int dinic()
{
int tot=0;
while(bfs()) tot+=dfs(0,inf);
return tot;
}
int read()
{
int x=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
void work()
{
for(int i=1;i<=tot;++i)
for(int j=h[i];j;j=c[j].x)
if(c[j^1].dis&&c[j].y)
printf("%d %d\n",id[i],id2[c[j].y-tot]);
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
a[i][j]=read();
for(int i=1;i<=n;i++)
{
id[++tot]=i;
for(int j=1;j<=m;j++)
{
if(a[i][j]==2) ++tot;
else colr[i][j]=tot;
id[tot]=i;
}
}
for(int i=1;i<=m;i++)
{
id2[++TOT]=i;
for(int j=1;j<=n;j++)
{
if(a[j][i]==2) ++TOT;
else colc[j][i]=TOT+tot;
id2[TOT]=i;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!a[i][j])
{
if(!use[colr[i][j]])
{
add(0,colr[i][j],1);
use[colr[i][j]]=1;
}
if(!use[colc[i][j]])
{
add(colc[i][j],t,1);
use[colc[i][j]]=1;
}
add(colr[i][j],colc[i][j],1);
}
printf("%d\n",dinic());
work();
return 0;
}

