[NOI2008]志愿者招募

题目

题目描述

申奥成功后，布布经过不懈努力，终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题：为即将启动的奥运新项目招募一批短期志愿者。经过估算，这个项目需要N 天才能完成，其中第i 天至少需要Ai 个人。布布通过了解得知，一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天，招募费用是每人Ci 元。新官上任三把火，为了出色地完成自己的工作，布布希望用尽量少的费用招募足够的志愿者，但这并不是他的特长！于是布布找到了你，希望你帮他设计一种最优的招募方案。

输入输出格式

输入格式：

第一行包含两个整数N, M，表示完成项目的天数和可以招募的志愿者的种类。接下来的一行中包含N 个非负整数，表示每天至少需要的志愿者人数。接下来的M 行中每行包含三个整数Si, Ti, Ci，含义如上文所述。为了方便起见，我们可以认为每类志愿者的数量都是无限多的。

输出格式：

仅包含一个整数，表示你所设计的最优方案的总费用。

输入输出样例

输入样例#1：

输出样例#1：

说明

1 ≤ N ≤ 1000，1 ≤ M ≤ 10000，题目中其他所涉及的数据均不超过2^31-1。

题解

鬼畜的建图方式……

本来我是想源点连志愿者、志愿者连控制的时间段（区间）、时间段连汇点的……

源点连第一天，汇点连最后一天，容量为$inf$费用为$0$

这样跑网络流是沿着时间流的（就是依次解决每一天的问题）

然后每一天向后一天连一条容量为$inf-a_i$，费用为$0$的边

为什么容量为$INF-a_i$？

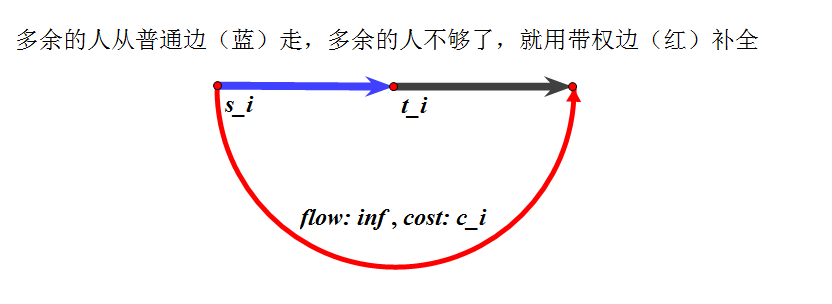
这就相当于少了$a_i$，得用带权边补全$inf$

志愿者连续干时沿这条边跑，因为连续干不花钱，所以优先选这种边

然后将每一类志愿者$s_i$与$t_i+1$连一条容量为$inf$花费为$c_i$的边，当连续干的人不够时，就得充钱使劲往里塞人补全$inf$

如图

代码

# include<iostream>
# include<cstdio>
# include<cstring>
# include<queue>
using namespace std;
const int MAX=2e6+1,INF=1e7,t=2e6;
struct p{
    int x,y,dis,cn;
}c[MAX<<2];
int n,m,num,tot1;
int d[MAX],h[MAX],pre[MAX];
bool use[MAX];
void add(int x,int y,int dis,int cn)
{
    c[num].x=h[y],c[num].y=x,c[num].dis=0,c[num].cn=-cn,h[y]=num++;
    c[num].x=h[x],c[num].y=y,c[num].dis=dis,c[num].cn=cn,h[x]=num++;
}
void EK()
{
    while(1)
    {
        queue<int> qu;
        qu.push(0);
        memset(pre,0,sizeof(pre));
        memset(d,1,sizeof(d));
        d[0]=0;
        while(!qu.empty())
        {
            int tt=qu.front();
            qu.pop();
            use[tt]=0;
            for(int i=h[tt];i;i=c[i].x)
              if(c[i].dis&&d[c[i].y]>d[tt]+c[i].cn)
              {
                  d[c[i].y]=d[tt]+c[i].cn;
                  pre[c[i].y]=i;
                  if(!use[c[i].y])
                  {
                      use[c[i].y]=1;
                      qu.push(c[i].y);
                }
              }
        }
        if(d[t]>INF) return;
        int sum=INF,hh=t;
        while(pre[hh])
        {
            int l=pre[hh];
            sum=min(sum,c[l].dis);
            hh=c[l^1].y;
        }
        hh=t;
        while(pre[hh])
        {
            int l=pre[hh];
            c[l].dis-=sum;
            c[l^1].dis+=sum;
            tot1+=sum*c[l].cn;
            hh=c[l^1].y;
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
      {
          int x;
          scanf("%d",&x);
          add(i,i+1,INF-x,0);
      }
    add(0,1,INF,0);
    add(n+1,t,INF,0);
    for(int i=1;i<=m;i++)
      {
          int x,y,dis;
          scanf("%d%d%d",&x,&y,&dis);
          add(x,y+1,INF,dis);
      }
    EK();
    printf("%d",tot1);
    return 0;
}

题目