[AHOI2009]最小割

题目

题目描述

A,B两个国家正在交战，其中A国的物资运输网中有$N$个中转站，$M$条向道路。设其中第$(1\leq i\leq M)$条道路连接了$v_i,u_i$两个中转站，那么中转站$v_i$可以通过该道路到达$u_i$中转站，如果切断这条道路，需要代价$c_i$。

现在B国想找出一个路径切断方案，使中转站$s$不能到达中转站$t$，并且切断路径的代价之和最小。

小可可一眼就看出，这是一个求最小割的问题。但爱思考的小可可并不局限于此。现在他对每条单向道路提出两个问题：

问题一：是否存在一个最小代价路径切断方案，其中该道路被切断？

问题二：是否对任何一个最小代价路径切断方案，都有该道路被切断？

现在请你回答这两个问题。

输入输出格式

输入格式：

第一行有$4$个正整数，依次为$N,M,s,t$。

第$2$行到第$(M+1)$行每行$3$个正整数$v,u,c$表示$v$中转站到$u$中转站之间有单向道路相连，单向道路的起点是$v$，终点是$u$,切断它的代价是$c(1\leq c\leq 100000)$。

注意:两个中转站之间可能有多条道路直接相连。同一行相邻两数之间可能有一个或多个空格。

输出格式：

$M$对每条单向边，按输入顺序，依次输出一行，包含两个非$0$即$1$的整数，分别表示对问题一和问题二的回答(其中输出$1$表示是，输出$0$表示否)。同一行相邻两数之间用一个空格隔开，每行开头和末尾没有多余空格。

输入输出样例

输入样例#1：

输出样例#1：

说明

测试数据规模如下表所示

数据编号	N	M	数据编号	N	M
1	10	50	6	1000	20000
2	20	200	7	1000	40000
3	200	2000	8	2000	50000
4	200	2000	9	3000	60000
5	500	20000	10	4000	60000

题解

似乎有几个性质：

1.残余网络中有剩余流量的边一定不在最小割中

如果有剩余流量的话肯定还有更优解

如图：

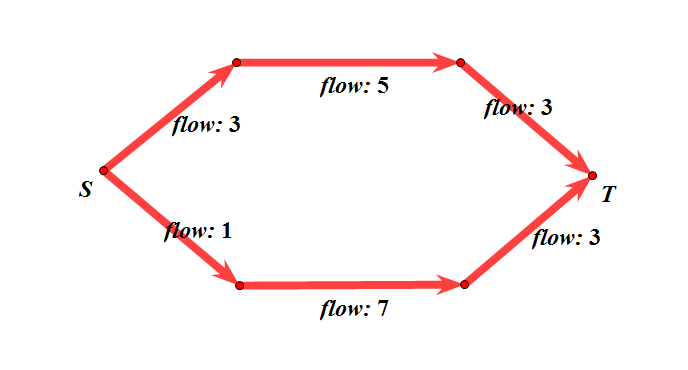
最小割为$4$，容量为$5$的边有剩余流量，它不在最小割里

2.残余网络中一条边（满足性质$1$）的首尾还能相互到达，那么这条边不满足条件$1$

我个人理解是一边的两点还能相互到达，说明它们在割后的同一点集合中

连接它们的边就肯定不是最小割方案，反之连接它们的边就肯定在某个最小割方案中

3.在残余网络中一边（满足性质$1$）的首尾分别与$S$和$T$在一个强连通分量中，那么这条边满足条件$2$

很好证明吧……

你如果不割这条边，最大流（即最小割）肯定得改变

性质$2,3$都是在性质$1$的基础上进行的，性质$2$不满足性质$3$肯定也不满足

至于是否联通，用$Tarjan$判断就行了~~我想用并查集失败了~~

代码

# include<iostream>
# include<cstdio>
# include<cstring>
# include<queue>
# include<stack>
# define ini inline int
# define inv inline void
# define inb inline bool
using namespace std;
const int MAX=4e3+1,inf=1e8;
struct p{
    int fr,x,y,dis;
}c[MAX<<5];
int n,m,s,t,num,TOT,ans,cnt;
int h[MAX],d[MAX],col[MAX],dfn[MAX],low[MAX];
bool use[MAX];
stack<int> st;
ini read()
{
    int x=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch))
    {
        x=x*10+ch-48;
        ch=getchar(); 
    }
    return x;
}
inv add(int x,int y,int dis)
{
    c[num].fr=y,c[num].x=h[y],c[num].y=x,c[num].dis=0,h[y]=num++;
    c[num].fr=x,c[num].x=h[x],c[num].y=y,c[num].dis=dis,h[x]=num++;
}
inb bfs()
{
    queue<int> qu;
    memset(d,0,sizeof(d));
    d[s]=1;
    qu.push(s);
    while(!qu.empty())
    {
        int tt=qu.front();
        qu.pop();
        for(int i=h[tt];i;i=c[i].x)
          if(!d[c[i].y]&&c[i].dis)
          {
          	d[c[i].y]=d[tt]+1;
          	qu.push(c[i].y);
          }
    }
    return d[t];
}
int dfs(int x,int dix)
{
    if(x==t||!dix) return dix;
    int sum=0;
    for(int i=h[x];i;i=c[i].x)
      if(d[c[i].y]==d[x]+1&&c[i].dis)
      {
      	int dis=dfs(c[i].y,min(dix,c[i].dis));
      	if(dis)
      	{
      		sum+=dis;
      		dix-=dis;
      		c[i].dis-=dis;
      		c[i^1].dis+=dis;
      		if(!dix) break;
        }
      }
    if(!sum) d[x]=-1;
    return sum;
}
inv dinic()
{
    while(bfs()) dfs(s,inf);
}
void tarjan(int x)
{
    dfn[x]=low[x]=++cnt;
    use[x]=1;
    st.push(x);
    for(int i=h[x];i;i=c[i].x)
      if(c[i].dis)
      if(!dfn[c[i].y])
      tarjan(c[i].y),low[x]=min(low[x],low[c[i].y]);
      else if(use[c[i].y])
      low[x]=min(low[x],dfn[c[i].y]);
    if(low[x]==dfn[x])
    {
        ans++;
        int tt=-1;
        while(tt!=x)
        {
            tt=st.top();
            st.pop();
            col[tt]=ans;
            use[tt]=0;
        }
    }
}
int main()
{
    n=read(),m=read(),s=read(),t=read();
    for(int i=1;i<=m;i++)
      {
      	int x=read(),y=read(),dis=read();
      	add(x,y,dis);
      }
    dinic();
    for(int i=1;i<=n;i++)
      if(!dfn[i]) tarjan(i);
    for(int i=1;i<num;i+=2)
      {
        if(c[i].dis)
      	{
      		printf("0 0\n");
      		continue;
        }
      	if(col[c[i].fr]==col[c[i].y])
      	printf("0 ");
      	else printf("1 ");
      	if(col[c[i].fr]==col[s]&&col[c[i].y]==col[t])
      	printf("1\n");
      	else printf("0\n");
      }
    return 0;
}

题目