[国家集训队]happiness

题目

题目描述

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。

作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

输入输出格式

输入格式：

第一行两个正整数n，m。

接下来是六个矩阵

第一个矩阵为n行m列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。

第二个矩阵为n行m列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。

第三个矩阵为n-1行m列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。

第四个矩阵为n-1行m列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。

第五个矩阵为n行m-1列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。

第六个矩阵为n行m-1列此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

输出格式：

输出一个整数，表示喜悦值总和的最大值

输入输出样例

输入样例#1：

输出样例#1：

说明

【样例说明】

两人都选理，则获得100+110+1000的喜悦值。

对于100%以内的数据，n,m<=100 所有喜悦值均为小于等于5000的非负整数

题解

考虑记录总量再求最小割

对于每个点，$S$（源点）与ta连一条容量为选文的边，$T$（汇点）与ta连一条容量为选理的边

建立新节点，$S$与新节点连一条容量为前后桌同时选文的边

新节点再分别与前后桌连一条容量为$inf$的边（为了不影响答案）

再建一个新节点，新节点与t连一条容量为前后桌同时选理的边

前后桌再与新节点连一条容量为$inf$的边

左右桌同理

这时跑最小割（也就是最大流），得到的是最小得不到的快乐值

所以所有快乐值-最小割就是答案

样例的图：

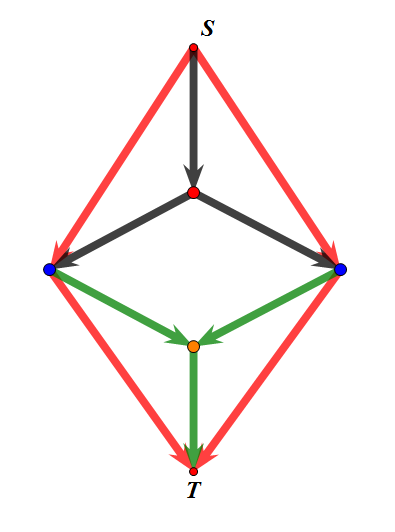
图中红点为第一个新建的点，橙点为第二个新建的点，蓝点为原来的点，跑最小割为$3$

代码

# include<iostream>
# include<cstdio>
# include<cstring>
# include<cstdlib>
# include<queue>
# define pu(x,y) (x-1)*m+y
using namespace std;
const int MAX=2e5+1,inf=1e8,t=2e5;
struct p{
    int x,y,dis;
}c[MAX<<1];
int n,m,num,SUM;
int h[MAX],d[MAX];
void add(int x,int y,int dis)
{
    c[num].x=h[y],c[num].y=x,c[num].dis=0,h[y]=num++;
    c[num].x=h[x],c[num].y=y,c[num].dis=dis,h[x]=num++;
}
bool bfs()
{
    memset(d,0,sizeof(d));
    queue<int> qu;
    qu.push(0);
    d[0]=1;
    while(!qu.empty())
    {
        int tt=qu.front();
        qu.pop();
        for(int i=h[tt];i;i=c[i].x)
          if(!d[c[i].y]&&c[i].dis)
          {
              d[c[i].y]=d[tt]+1;
              qu.push(c[i].y);
          }
    }
    return d[t];
}
int dfs(int x,int dix)
{
    if(!dix||x==t) return dix;
    int sum=0;
    for(int i=h[x];i;i=c[i].x)
      if(c[i].dis&&d[c[i].y]==d[x]+1)
      {
          int dis=dfs(c[i].y,min(dix,c[i].dis));
          if(dis)
          {
              dix-=dis;
              sum+=dis;
              c[i].dis-=dis;
              c[i^1].dis+=dis;
              if(!dix) break;
        }
      }
    if(!sum) d[x]=-1;
    return sum;
}
int dinic()
{
    int tot=0;
    while(bfs()) tot+=dfs(0,inf);
    return tot;
}
int main()
{
    scanf("%d%d",&n,&m);
    int ss=pu(n,m);
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        {
            int dis,tt=pu(i,j);
            scanf("%d",&dis);
            SUM+=dis;
            add(0,tt,dis);
        }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        {
            int dis,tt=pu(i,j);
            scanf("%d",&dis);
            SUM+=dis;
            add(tt,t,dis);
        }
    for(int i=1;i<n;i++)
      for(int j=1;j<=m;j++)
        {
            int dis,tt=pu(i,j)+ss,t1=pu(i,j),t2=pu(i+1,j);
            scanf("%d",&dis);
            SUM+=dis;
            add(0,tt,dis);
            add(tt,t1,inf);
            add(tt,t2,inf);
        }
    for(int i=1;i<n;i++)
      for(int j=1;j<=m;j++)
        {
            int dis,tt=pu(i,j)+2*ss,t1=pu(i,j),t2=pu(i+1,j);
            scanf("%d",&dis);
            SUM+=dis;
            add(tt,t,dis);
            add(t1,tt,inf);
            add(t2,tt,inf);
        }
    for(int i=1;i<=n;i++)
      for(int j=1;j<m;j++)
        {
            int dis,tt=pu(i,j)+3*ss,t1=pu(i,j),t2=pu(i,j+1);
            scanf("%d",&dis);
            SUM+=dis;
            add(0,tt,dis);
            add(tt,t1,inf);
            add(tt,t2,inf);
        }
    for(int i=1;i<=n;i++)
      for(int j=1;j<m;j++)
        {
            int dis,tt=pu(i,j)+4*ss,t1=pu(i,j),t2=pu(i,j+1);
            scanf("%d",&dis);
            SUM+=dis;
            add(tt,t,dis);
            add(t1,tt,inf);
            add(t2,tt,inf);
        }
    printf("%d",SUM-dinic());
    return 0;
}

题目