题目
题目背景
阿狸喜欢收藏各种稀奇古怪的东西,最近他淘到一台老式的打字机。
题目描述
打字机上只有28个按键,分别印有26个小写英文字母和’B’、’P’两个字母。经阿狸研究发现,这个打字机是这样工作的:
·输入小写字母,打字机的一个凹槽中会加入这个字母(这个字母加在凹槽的最后)。
·按一下印有’B’的按键,打字机凹槽中最后一个字母会消失。
·按一下印有’P’的按键,打字机会在纸上打印出凹槽中现有的所有字母并换行,但凹槽中的字母不会消失。
例如,阿狸输入aPaPBbP,纸上被打印的字符如下:
a aa ab 我们把纸上打印出来的字符串从1开始顺序编号,一直到n。打字机有一个非常有趣的功能,在打字机中暗藏一个带数字的小键盘,在小键盘上输入两个数(x,y)(其中1≤x,y≤n),打字机会显示第x个打印的字符串在第y个打印的字符串中出现了多少次。
阿狸发现了这个功能以后很兴奋,他想写个程序完成同样的功能,你能帮助他么?
输入输出格式
输入格式:
输入的第一行包含一个字符串,按阿狸的输入顺序给出所有阿狸输入的字符。
第二行包含一个整数m,表示询问个数。
接下来m行描述所有由小键盘输入的询问。其中第i行包含两个整数x, y,表示第i个询问为(x, y)。
输出格式:
输出m行,其中第i行包含一个整数,表示第i个询问的答案。
输入输出样例
输入样例#1:
aPaPBbP
3
1 2
1 3
2 3
输出样例#1:
2
1
0
说明
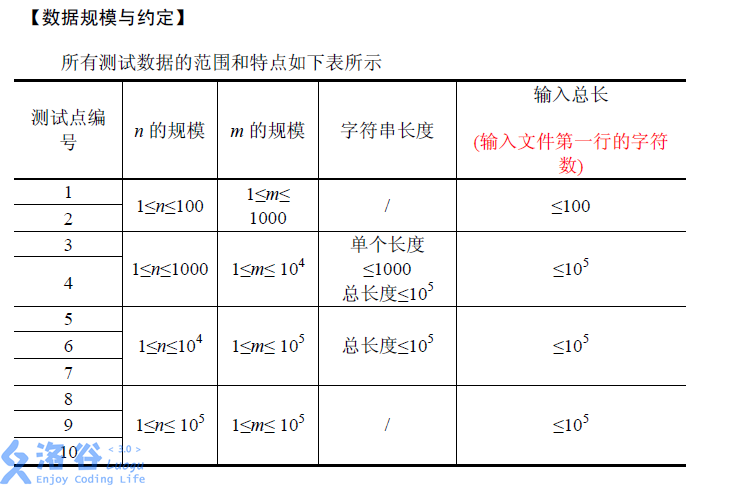
数据范围:
对于100%的数据,n<=100000,m<=100000,第一行总长度<=100000。
题解
这题好妙啊…
首先这题$40$分暴力做法是$kmp$直接匹配
我们考虑同样作为字符串匹配算法的$AC$自动机
可以发现$fail$指针有一个神奇的性质:
如果一个字符串$a$的最后一位的$fail$指向字符串$b$的一个字符,那么$a$肯定包含$b$
所以原问题就可以转化为统计$x$最后一位在$fail$树里的子树里有多少$y$的字符
树结构+子树求和,想到了什么?
$dfs$序+线段树就可以搞了
所以按照原来的$Tire$树向下找,顺便在$dfs$序上标记
将询问离线,按$y$值排序,遍历字符串
然后对于每一个'P',因为这是打印,统计当前结尾对应的$y$所对应的询问,里面的$x$的子树和(好绕)
对于每一个'B',因为这是删除,所以讲当前节点的$dfs$序对应的值$-1$,并返回到ta的父节点
对于其他,对应的$dfs$序$+1$,然后就离线输出就行了
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<queue>
# include<algorithm>
# define mid (l+r>>1)
# define tl (k<<1)
# define tr (k<<1|1)
using namespace std;
const int MAX=1e5+1;
struct p{
int x,y;
}c[MAX];
struct q{
int x,y,id;
bool operator< (const q &a)
const{
return y<a.y;
}
}qu[MAX];
int num,n,L,TOT,cnt,sum;
int h[MAX],ov[MAX],ans[MAX];
string a;
void add(int x,int y)
{
c[++num]=(p){h[x],y},h[x]=num;
}
struct Tire{
int fail[MAX],fa[MAX],die[MAX],id[MAX],siz[MAX];
int vis[MAX][26],use[MAX][26];
struct o{
int x;
}s[MAX<<2];
void build()
{
int x=0;
for(int i=0;i<L;++i)
{
if(a[i]=='B')
x=fa[x];
else if(a[i]=='P')
ov[++cnt]=x;
else
{
if(!vis[x][a[i]-'a'])
use[x][a[i]-'a']=vis[x][a[i]-'a']=++TOT,fa[TOT]=x;
x=vis[x][a[i]-'a'];
}
}
}
void GET_FAIL()
{
queue<int> qu;
for(int i=0;i<26;i++)
{
int v=vis[0][i];
if(v) qu.push(v);
}
while(!qu.empty())
{
int tt=qu.front();
qu.pop();
for(int i=0;i<26;i++)
{
int v=vis[tt][i];
if(v)
{
fail[v]=vis[fail[tt]][i];
qu.push(v);
}
else vis[tt][i]=vis[fail[tt]][i];
}
}
}
void dfs(int x)
{
id[x]=++sum,siz[x]=1;
for(int i=h[x];i;i=c[i].x)
{
int y=c[i].y;
if(y==x) continue;
dfs(y);
siz[x]+=siz[y];
}
}
void pus(int k)
{
s[k].x=s[tl].x+s[tr].x;
}
int ask(int l,int r,int k,int L,int R)
{
if(l==L&&r==R) return s[k].x;
if(R<=mid) return ask(l,mid,tl,L,R);
if(L>mid) return ask(mid+1,r,tr,L,R);
return ask(l,mid,tl,L,mid)+ask(mid+1,r,tr,mid+1,R);
}
void change(int l,int r,int k,int x,int dis)
{
if(l==r)
{
s[k].x+=dis;
return;
}
if(x<=mid) change(l,mid,tl,x,dis);
else change(mid+1,r,tr,x,dis);
pus(k);
}
void GET_ANS()
{
int tot=1,tot1=0;
int x=0;
for(int i=0;i<L;++i)
{
if(a[i]=='P')
{
tot1++;
while(qu[tot].y==tot1)
{
int xe=qu[tot].x;
ans[qu[tot].id]=ask(1,sum,1,id[ov[xe]],id[ov[xe]]+siz[ov[xe]]-1);
++tot;
}
}
else if(a[i]=='B')
change(1,sum,1,id[x],-1),x=fa[x];
else
x=use[x][a[i]-'a'],change(1,sum,1,id[x],1);
}
}
}Tree;
int read()
{
int x=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x;
}
int main()
{
cin>>a;
L=a.length();
Tree.build();
n=read();
for(int i=1;i<=n;++i)
qu[i].x=read(),qu[i].y=read(),qu[i].id=i;
sort(qu+1,qu+1+n);
Tree.GET_FAIL();
for(int i=0;i<=TOT;++i)
add(Tree.fail[i],i);
Tree.dfs(0);
Tree.GET_ANS();
for(int i=1;i<=n;++i)
printf("%d\n",ans[i]);
return 0;
}

