题目
题目描述
Bob有一棵n个点的有根树,其中1号点是根节点。Bob在每个点上涂了颜色,并且每个点上的颜色不同。
定义一条路径的权值是:这条路径上的点(包括起点和终点)共有多少种不同的颜色。
Bob可能会进行这几种操作:
1 x 把点x到根节点的路径上所有的点染上一种没有用过的新颜色。
2 x y 求x到y的路径的权值。
3 x 在以x为根的子树中选择一个点,使得这个点到根节点的路径权值最大,求最大权值。
Bob一共会进行m次操作
输入输出格式
输入格式:
第一行两个数n,m。
接下来n-1行,每行两个数a,b,表示a与b之间有一条边。
接下来m行,表示操作,格式见题目描述
输出格式:
每当出现2,3操作,输出一行。
如果是2操作,输出一个数表示路径的权值
如果是3操作,输出一个数表示权值的最大值
输入输出样例
输入样例#1:
5 6
1 2
2 3
3 4
3 5
2 4 5
3 3
1 4
2 4 5
1 5
2 4 5
输出样例#1:
3
4
2
2
说明
共10个测试点
测试点1,$1\leq n,m\leq 1000$
测试点2、3,没有2操作
测试点4、5,没有3操作
测试点6,树的生成方式是,$对于i(2\leq i\leq n)$,在1到$i−1$中随机选一个点作为$i$的父节点。
测试点7,$1\leq n,m\leq 50000$
测试点8,$1\leq n\leq 50000$
测试点9,10,无特殊限制
对所有数据,$1\leq n\leq 10^5,1\leq m\leq 10^5$
时间限制:1s
空间限制:128MB
题解
恶心题为什么SD光出这种题。。。
总的来说就是$LCT$+树链剖分+树上差分
先不管操作$1$
对于操作2,考虑树上差分,设$s[i]$为$i$点到根的权值和,则答案就是$s_x+s_y-2s_{lca(x,y)}+1$(多减了$1$个$lca$所以+1)
那么每个点的初始值就是ta的深度(因为开始每个点颜色都不一样)
发现上面的关系可以用树链剖分来解决
求出$lca$后单点查询$x,y,lca$的权值就可以解决操作2
操作3求子树最大值也是树链剖分的基本操作
主要问题是操作$1$
操作1就很妙了,利用了一个性质:(以下注意链和边的区分)
$LCT$中实链数量(即$splay$的数量)=虚边数量+1
我们把同一颜色的点放在$1$个$splay$里
由操作可得,$LCT$中点$i$到根节点有多少实链$s_i$就是多少
所以$access$将几个$splay$连成1个$splay$,正好对应着用同一种颜色覆盖路径
然后$access$的时候如果一条边由虚变实(即虚边减少),这条边连的深度较大的点的子树每个点的$s-1$
如果一条边由实变虚(即虚边增加),这条边连的深度较大的点的子树每个点的$s+1$
如图:
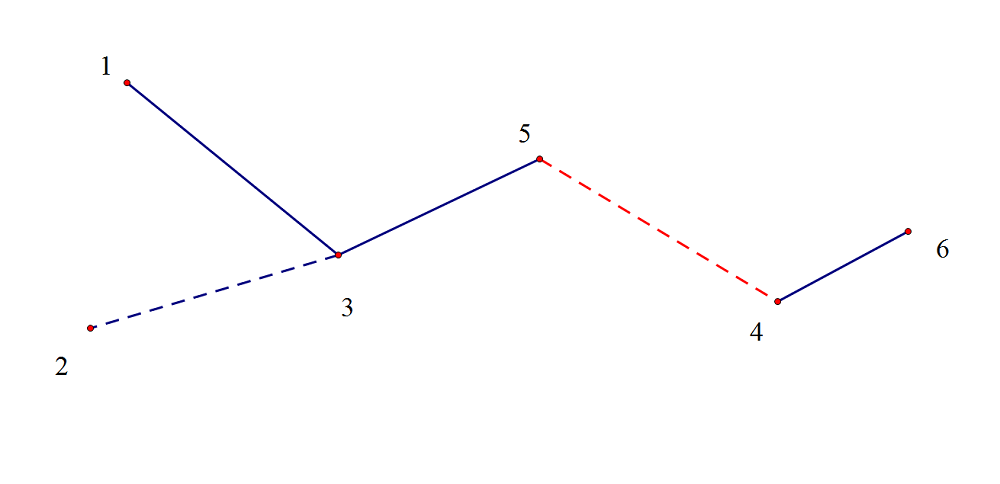
设6号点为根,图中红色虚边要变成实边,深度较大的节点是5(4号红边怎么变跟ta没关系)
5点的相连的实链合并了,但到根节点的实链总数没变,所以对应的s不变
1、2、3点到根的实链合并了,到根节点的实链总数-1,所以对应的$s-1$
实变虚同理自己yy即可
所以$access$时要加上树链剖分的区间修改操作
还有$LCT$中要保存当前节点在树中最左儿子的编号用以修改区间(即代码中$LCT$的$w_i$)
于是这道毒瘤+码农题就解决了
代码
# include<iostream>
# include<cstring>
# include<cstdio>
# include<cstdlib>
# define mid (l+r>>1)
# define tl (k<<1)
# define tr (k<<1|1)
using namespace std;
const int MAX=1e5+1;
struct p{
int x,y;
}c[MAX<<1];
int n,m,num,cnt,tot,rt;
int h[MAX],ID[MAX],top[MAX],d[MAX],fa[MAX],son[MAX],siz[MAX];
struct Segment_Tree{
struct q{
int x,lazy;
}s[MAX<<2];
void pus(int k)
{
s[k].x=max(s[tl].x,s[tr].x);
}
void down(int k)
{
int f=s[k].lazy;
s[k].lazy=0;
if(!f) return;
s[tl].lazy+=f,s[tr].lazy+=f;
s[tl].x+=f,s[tr].x+=f;
}
void change(int l,int r,int k,int L,int R,int dis)
{
if(l==L&&r==R)
{
s[k].x+=dis,s[k].lazy+=dis;
return;
}
down(k);
if(R<=mid) change(l,mid,tl,L,R,dis);
else if(L>mid) change(mid+1,r,tr,L,R,dis);
else
{
change(l,mid,tl,L,mid,dis);
change(mid+1,r,tr,mid+1,R,dis);
}
pus(k);
}
void change1(int l,int r,int k,int x,int dis)
{
if(l==r)
{
s[k].x+=dis;
return;
}
down(k);
if(x<=mid) change1(l,mid,tl,x,dis);
else change1(mid+1,r,tr,x,dis);
pus(k);
}
int ask(int l,int r,int k,int L,int R)
{
if(l==L&&r==R)
return s[k].x;
down(k);
if(R<=mid) return ask(l,mid,tl,L,R);
else if(L>mid) return ask(mid+1,r,tr,L,R);
else return max(ask(l,mid,tl,L,mid),ask(mid+1,r,tr,mid+1,R));
}
int ask1(int l,int r,int k,int x)
{
if(l==r) return s[k].x;
down(k);
if(x<=mid) return ask1(l,mid,tl,x);
else return ask1(mid+1,r,tr,x);
}
}Tree1;
struct Link_Cut_Tree{
int fa[MAX],w[MAX];
int son[MAX][2];
bool fl[MAX];
bool is_root(int x)
{
return son[fa[x]][1]!=x&&son[fa[x]][0]!=x;
}
bool id(int x)
{
return son[fa[x]][0]==x?0:1;
}
void pus(int x)
{
if(son[x][0]) w[x]=w[son[x][0]];
else w[x]=x;
}
void down(int x)
{
if(x&&fl[x])
{
if(son[x][1]) fl[son[x][1]]^=1;
if(son[x][0]) fl[son[x][0]]^=1;
swap(son[x][1],son[x][0]);
fl[x]=0;
}
}
void rot(int x)
{
int y=fa[x],z=fa[y],k=id(x);
if(!is_root(y)) son[z][id(y)]=x;
son[y][k]=son[x][k^1],fa[son[y][k]]=y;
son[x][k^1]=y,fa[y]=x;
fa[x]=z;
pus(y),pus(x);
}
void PUS(int x)
{
if(!is_root(x)) PUS(fa[x]);
down(x);
}
void splay(int x)
{
PUS(x);
for(int y;!is_root(x);rot(x))
if(!is_root(y=fa[x]))
rot(id(x)==id(y)?y:x);
}
void access(int x)
{
for(int y=0;x;y=x,x=fa[x])
{
splay(x);
int hh=w[son[x][1]];
if(son[x][1]) Tree1.change(1,n,1,ID[hh],ID[hh]+siz[hh]-1,1);
hh=w[y];
if(y) Tree1.change(1,n,1,ID[hh],ID[hh]+siz[hh]-1,-1);
son[x][1]=y;
if(y) fa[y]=x;
}
}
}Tree2;
void add(int x,int y)
{
c[++num]=(p){h[x],y};h[x]=num;
c[++num]=(p){h[y],x},h[y]=num;
}
void dfs(int x,int f)
{
fa[x]=f,d[x]=d[f]+1,siz[x]=1;
for(int i=h[x];i;i=c[i].x)
{
int y=c[i].y;
if(y==f) continue;
dfs(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
void dfs1(int x,int tp)
{
top[x]=tp,ID[x]=++cnt;
if(son[x]) dfs1(son[x],tp);
else return;
for(int i=h[x];i;i=c[i].x)
{
int y=c[i].y;
if(y==fa[x]||y==son[x]) continue;
dfs1(y,y);
}
}
int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(d[x]>d[y]) swap(x,y);
return x;
}
int read()
{
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);f=(ch=='-')?-1:1,ch=getchar());
for(;isdigit(ch);x=x*10+ch-48,ch=getchar());
return x*f;
}
int main()
{
n=read(),m=read();
for(int i=1;i<n;i++)
{
int x=read(),y=read();
add(x,y);
}
dfs(1,0);
dfs1(1,1);
for(int i=1;i<=n;i++)
{
Tree1.change1(1,n,1,ID[i],d[i]);
Tree2.w[i]=i,Tree2.fa[i]=fa[i];
}
for(int i=1;i<=m;i++)
{
int op=read(),x,y;
if(op==1)
Tree2.access(read());
else if(op==2)
{
x=read(),y=read();
int lca=LCA(x,y);
int s1=Tree1.ask1(1,n,1,ID[x]),s2=Tree1.ask1(1,n,1,ID[y]),s3=Tree1.ask1(1,n,1,ID[lca]);
printf("%d\n",s1+s2-s3*2+1);
}
else if(op==3)
{
x=read();
printf("%d\n",Tree1.ask(1,n,1,ID[x],ID[x]+siz[x]-1));
}
}
return 0;
}

